Notes de cours pour section 2, chapitre 2.2 du cours SEG 2506
par
Gregor v. Bochmann, February 2004, révision importante en 2010, revisé en 2013 et 2015
Quand on parle de langages formels, on essaie de définir des règles simples et précises pour déterminer quelle séquence de symboles (caractères, lexèmes ou autre) est valide. C'est une approche mathématique qui permet de formaliser les définitions de langages qui se prêtent aux algorithmes de génération et de reconnaissance. Cette appoche peut être appliquée, séparément, à l'analyse lexicale et à l'analyse synrtaxique.
La définition d'un langage formel commence par la définition d'un alphabet A qui est un ensemble fini de symboles (on peut ici penser à des caractères ou à des lexèmes, par exemple). Ensuite on considère A* qui est l'ensemble de toutes les séquences (de longueur fini) de symboles de A, incluant la séquence vide (qui ne contient aucun symbole - écrite epsilon (є) ou lambda). Ces séquences sont aussi appelées des chaînes.
Définition: Un language sur A est un sous-ensemble de A*. - - Les éléments du langage sont appelé des séquences valides, ou les phrases du langages. Voici des exemples de langages (L1 à L4)
Étant donné un alphabet A, on a les opérations suivantes sur les séquences dans A*:
Concaténation (exemple: a b ou a . b )
Sur l'ensemble de tous les langages sur A (c'est-à-dire, les langages sur l'alphabet A, i.e. les sous-ensembles de A*), on peut utiliser les opérateur suivantes (voici les définitions du livre de Aho):
les opérateurs définis en général pour les ensembles (puisque un langage est un ensemble de séquences), comme
Une grammaire est un ensemble d'équations sur des langages, utilisant les opérateurs ci-hauts. Chaque équation a la forme "Y = Expression" où Y est une variable de langages, et Expression est une expression qui contient des chaînes (constantes) et variables de langages combinées par les opérateurs ci-hauts. Les chaînes constantes sont aussi appelées "séquences terminales"; elles sont des séquences de symboles de l'alphabet. Voici deux exemples de grammaires:
Grammaire G1 sur l'alphabet {a, b, c} (regulière) |
Grammaire G2 sur l'alphabet {x, y, z} (hors contexte) |
Définition: Une solution d'une grammaire est un ensemble de langages, un langage par variable de langage de la grammaire, tel que toutes les équations de la grammaire sont satisfaites. - - Le langage défini par une grammaire est le langage associé à la première variable de langage de la grammaire dans un solution de la grammaire. - Cette variable est aussi appelée la racine de la grammaire, ou le symbole de départ.
Définition: Deux grammaire sont équivalentes si elles définissent le même langage. (Révision: Une équivalence est une sorte de relation. - Quelles sont les trois propriétés mathématique d'une équivalence ?)
Notes:
La notation introduite ci-haute pour définir une grammaire comme un ensemble d'équations de langages est probablement la plus mathématique. Il ;y a d'autres notations (qui ont la même sémantique) qui sont souvent utilisées. Les plus importantes sont les suivantes:
Exemple de nombres: Nous considérons les nombres réels (basés sur le système ternaire, utilisant seulement les chiffres 0, 1 et 2) qui peuvent être vus comme un langage sur l'alphabet {0, 1, 2, . }. Nous supposons qu'un zéro (un seul) est requis avant le point décimal (i.e. ternaire) si le nombre est plus petit que 1. Des exemples de tels nombres sont: 0. , 0.010, 12. , 132.012 et des exemples de séquences ne faisant pas partie du langage sont: 123 , 01.2 . Une expression régulière représentant ces nombres réels est la suivante: (0 | (1 | 2) (0 | 1 | 2)* ) . (0 | 1 | 2)* . Voici d'autres examples simples.
Propriétés algébriques d'équivalence pour expressions régulières: Les équations d'équivalence suivantes peuvent être utilisées pour déterminer si deux expressions régulières données sont équivalentes (en substituant une côté d'une de ces équations dans une expression donnée par l'autre côté de l'équation, ainsi obtenant une expression équivalente à l'expression donnée). Par exemple, on peut utiliser l'équation (15) pour montrer que ((a | b ) c )* (a | b ) est équivalent à (a | b ) (c (a | b ))* .
Un AEF est une machine à états. Un de ces états est l'état initial et un sous-ensemble des états sont des états acceptants. L'entrée de l'automate est fournie par une tête de lecture qui lit une séquence de symboles de l'alphabet, un symbole à la fois, de gauche à droite. Chaque symbole lu représente une entrée à l'automate et donne lieu à une transition. Si dans l'état courant, l'automate n'a pas de transition pour le symbole lu, alors la chaîne n'est pas valide. Quand la tête de lecture arrive à la fin de la séquence d'entrée et l'automate est dans un état acceptant, alors la séquence qui a été lue est acceptée, c'est-à-dire, elle fait partie du langage défini par l'automate. Un tel automate est aussi appelé un automate accepteur. Nous faisons l'hypothèse que l'automate est déterministe, c'est-à-dire, après une chaîne lue, il peut être seulement dans un état unique. - Note: la seule différence avec un LTS est le fait qu'un sous-ensemble des états sont définis comme "acceptants".
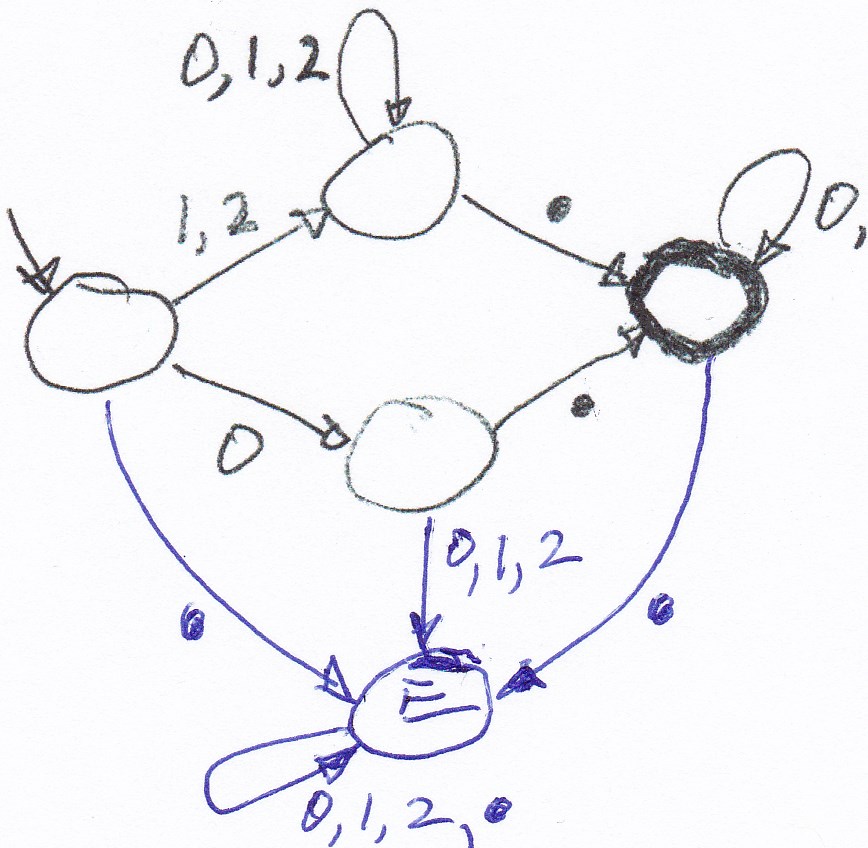
Des nombre réels: Un automate accepteur pour le langage des nombres réels (ternaires - considéré ci-haut) est donné par le diagramme de transition suivante. Les états acceptants sont en gras.
Le language Nombre-Pair-a:
Nous considérons le langage Nombre-Pair-a sur
l'alphabet {a, b, c, d} consistant de toutes les séquences qui
contiennent un nombre pair de symboles "a" et aucun
symbole "d". Voici un automate qui accepte ce langage:
Définition: On dit que deux automates sont équivalents s'il acceptent le même langage. (Note: Cette définition est très similaire à l'équivalence entre grammaires).
Exemple de deux automates équivalents: 
Un automate accepteur est un analyseur efficace pour déterminer si une chaîne de symboles fait partie du language défini par l'automate. Notez que dans chaque état de l'automate, le prochain symbole lu détermine directement la prochaine transition à exécuter; on dit que l'automate est déterministe. C'est pourquoi la complexité de l'analyse est O(n) où n est la longueur de la séquence d'entrée (il y aura une transition exécutée par symbole d'entrée). Alors, comment peut-on obtenir une vrai implantation d'un automate ? - Voici plusieurs stratégies:
public class Even_a_Acceptor { public Input read() {} |
Table des transitions d'un automate pour le langage Nombre-Pair-a Algorithme:
|
||||||||||||||||||||
| Java program qui accepte le langage Nombre-Pair-a |
Un AEF est un bon outil pour l'analyse lexical (supposant que les règles lexicales correspondent aux propriétés d'un automate), mais il reste un problème: Comment savoir quand la chaîne constituant un lexèmes est terminée et le prochain lexème commence? (Note: Dans les langues naturelles, c'est le caractère d'espace qui fait cette séparation, mais dans un programme on peut écrire "abc=23+a" - sans espace).
La solution normalement adopté pour résoudre ce problème est de définir le langage de tel manière que l'analyseur peut toujours chercher le lexème le plus longue possible. Dans l'exemple ci-haut, la chaîne "abc" sera alors un identificateur, et non pas trois identificateurs. Alors, pour savoir si le prochain caractère peut faire partie d'un lexème plus long, il est nécessaire de lire le prochain caractère. Et s'il ne peut pas être utilisé pour alonger l'unité lexicale en train d'être analysée, il faut le restituer pour qu'il soit pris en compte comme premier caractère pour le prochain lexème qui sera lu.
Dans l'exemple suivant, cette restitution est indiquée par un B ("to put back") dans l'état atteint. L'automate montré dans la figure ci-dessous distingue trois unités lexicales: des nombres décimaux avec point (real), l'opérateur de multiplication (mult) et l'opérateur d'exponentiation (exp). Un état accepteur (cercle gras) avec aucune transition suivante indique qu'un lexème de longueur maximale a été obtenu (retour au programme appelant). Un état étiquetté E indique qu'une erreur lexicale a été trouvée (dans cet exemple, un nombre plus grand ou égale à 1 ne doit pas commencer par le chiffre 0; e.g. la chaîne de caractères "01.0" n'est pas valable; et chaque nombre doit inclure un point).
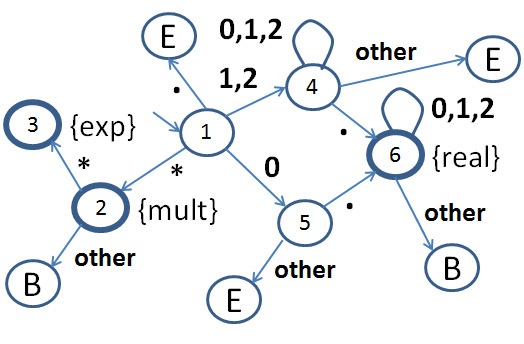
La table suivante est une table des transitions pour l'automate ci-haut. Pour chaque état (numéro de ligne) et chaque entrée reçue (colonne), la table contient de l'information sur le comportement de l'automate. L'information a deux parties. La première indique l'action à exécuter. Les cas possibles sont: une transition normale (next, prochain état); une situation d'erreur (error, ); le retour d'un lexème, cas normal (return, lexème); et le retour d'un lexème et la restitution du dernioer caractère (back, lexème).
| 0 | 1 | 2 | point | star | |
| 1 | (next, 5) | (next, 4) | (next, 4) | (error,) | (next, 2) |
| 2 | (back, mult) | (back, mult) | (back, mult) | (back, mult) | (return, exp) |
| 4 | (next, 4) | (next, 4) | (next, 4) | (next, 6) | (error,) |
| 5 | (error,) | (error,) | (error,) | (next, 6) | (error,) |
| 6 | (next, 6) | (next, 6) | (next, 6) | (back, real) | (back, real) |
Voici un programme en Java qui implémente un analyseur lexical utilisant une telle table de transitions.
Un outil assez connu, appelé Lex, a été construit pour générer un analyseur lexical (c'est-à-dire, un algorithme d'analyse) écrit en C (pour être incorporé dans un compilateur écrit en C) à partir d'une description des règles lexicales du langage en termes d'expressions régulières. D'autres outils similaire existent aussi pour d'autres langages d'implantation, comme Java. Similairement, il existent des outils pour la génération d'analyseur syntaxiques à partir d'une description des règles syntaxique en forme d'une grammaire. En général, de tels outils sont appelés "compiler writing systems" ou générateurs de compilateurs. Ils automatisent assez bien les aspects de l'analyse lexicale et syntaxique du langage à compiler, mais les facilités pour automatiser la génération de code sont souvent assez rudimentaire.
Le diagramme suivant montre les étapes pour l'utilisation d'un générateur de compilateur (ici en occurrence, Lex):
Le langage d'entrée utilisé par l'outil Lex pour décrire les règles lexicales admet certains extensions aux expressions régulières de base discutées ci-haut. En particulier, plusieurs catégories lexicales peuvent être définis, chacune par une expression régulière. Les "définitions régulières" sont aussi supportées (voir ci-haut). Des notations, quelquefois appelées "regex", assez similaire sont utilisées par des outils divers, comme l'outil grep sous Unix, la classe Pattern en Java ou les facilités de langages comme Perl ou Ruby.
Dans ce qui suit, nous voulons comprendre les principles qui permettent à l'outil Lex de créer un programme qui fait l'analyse lexicale correspondant à des expressions régulières données en entrée. Le principe est de trouver un automate qui accepte les sequences définies par les expressions régulières. Donc, il s'agit de savoir comment on peut obtenir un automate déterministe qui accepte exactement les chaînes d'un langage défini par une expression régulière donnée. Mais il y a problème: Nous allons voir qu'une expression régulière nous amene naturellement à un automate accepteur non déterministe. Puisqu'un tel automate n'admet pas une implantation efficace, il faut savoir si (et comment) un peut trouver un automate déterministe equivalent à un automate non déterministe donné. Tout cela sera discuté dans ce qui suit.
Dans la suite, nous considérons le problème suivant: Étant donné une expression régulière qui définit un langage régulier, trouver un automate qui accepte le même langage. Prenons par exemple l'expression (ab)* ac; c' est-à-dire le language des séquences qui commencent par zéro ou plusieurs fois "a b" et terminées par "a c". Utilisant notre intuition, nous pouvons proposer l'automate suivant comme solution:
Malheureusement, cet automate est non déterministe (il a deux transitions "a" de l'état initial). C'est pouquoi une implantation directe de cet automate impliquerait des essais et retours en arrière ("backtracking"). Cela donne en général une grande complexité de calcul et sera inefficace.
Dans cette sous-section, nous allons étudier les deux questions suivantes:
Définition: Un automate est déterministe si pour chaque état et chaque symbole d'entrée donnés, il y a au maximum une transition possible. (Note: S'il n'y a pas de transition, ce symbole ne peut être accepté dans l'état en question.)
Définition: Un automate est non déterministe, si dans un état donné, il y a plusieurs transitions possible pour le même symbole d'entrée vers des états différents, ou si l'automate contient une transition spontanée, c'est-à-dire, une transition qui peut s'effectuer sans lecture d'un symbole d'entrée. Note: Une transition spontanée est normalement étiquettée par є.
Définition: Une séquence de symboles de l'alphabet est acceptée par un automate non déterministe, s'il existe un pas d'exécution possible de l'automate qui amène l'automate, à la fin de l'analyse, dans un état acceptant.
Rappel: Définition: Deux automates sont équivalents s'ils acceptent le même langage.
Note: Although the definition of a non-deterministic automaton is nearly identical to the definition of an LTS, there is an important difference in using them. LTS are normally models of state machines that can make non-deterministic choices (and only one execution path will be considered at a given time), while for nondeterministic automata, all possible execution paths will be explored in parallel in order to see whether a given sequence of symbols can be accepted.
Le diagramme ci-dessous montre un automate non déterministe qui accepte le langage défini par l'expression régulière (a | b)* a b b .
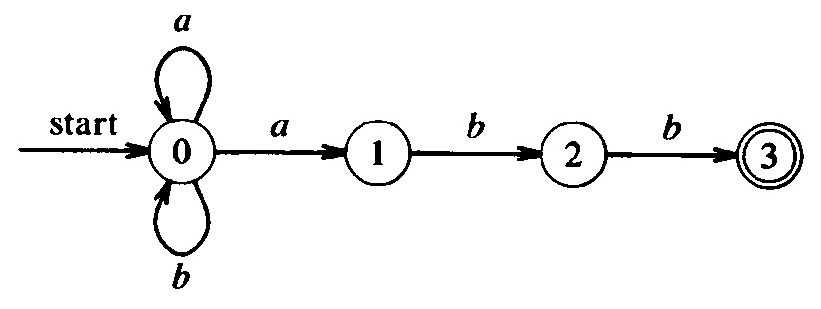Table des transitions:
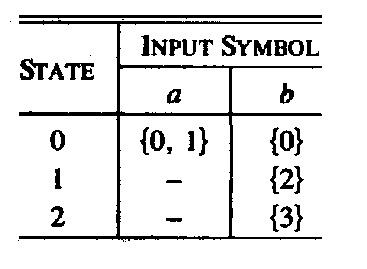
L'automate ci-haut est équivalent à l'automate ci-dessous (qui accepte le même langage). Note: Vous voyez que la structure de l'automate non déterministe est plus simple; elle correspond directement à l'expression régulière.
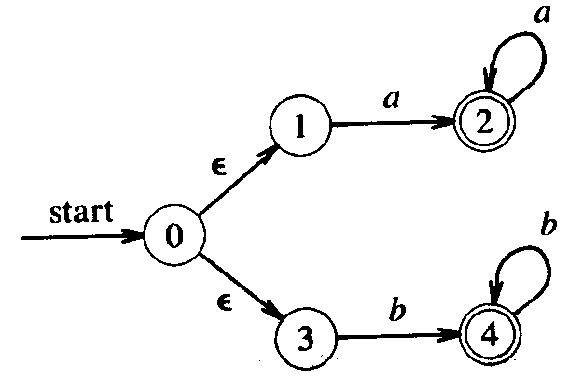
Le diagramme de transition ci-dessous montre un automate non déterministe qui accepte le langage défini par l'expression régulière a a* | b b*.
Les automates non déterministes ne sont pas très utiles pour réaliser des algorithmes d'analyse (parce que pas efficace - en contrast avec les automates déterministe, voir discussions ci-haut). Par contre, les automates non déterministes sont souvent plus aptes à représenter certains langages. Par exemple, il est assez évident que le premier automate de l'exemple (a) ci-haut (non déterministe) accepte le langage défini par (a | b)* a b b ; tandis que ce fait est difficile à voir pour le deuxième automate (déterministe).
L'idée de l'algorithme de conversion (bien connu en informatique, et expliqué dans le livre de Aho et al.) est que l'on peut considérer l'analyse d'une chaîne de symboles par l'automate non déterministe comme un traitement parallèle: Si un automate déterministe, après avoir analysé un préfixe de la chaîne, est dans un état spécifique, l'automate non déterministe pourrait être dans un certain sous-ensemble de ses états (en fonction des différents pas de transitions qui étaient possibles pour les symboles d'entrée lors de l'analyse du préfixe). Dans un sens, l'algorithme de construction de l'automate déterministe équivalent considère (pendant le temps de conception) toutes les transitions que l'automate non déterministe pourrait exécuter pendant l'analyse d'une séquence d'entrée donnée.
Étant donné un automate non déterministe N et un automate déterministe D équivalent à construire. Nous commençons avec l'état initial (avant qu'un entrée soit lue). N pourrait être dans n'importe quel état qui est accessible de son état initial par des transitions spontanées seulement. Ce sous-ensemble d'états correspond à l'état initial de D. Supposant maintement qu'un préfix de la séquence d'entrée est déjà lu et x est le prochain symbole à lire. N pourrait être dans un sous-ensemble de ses états, et ce sous-ensemble correspond à l'état dans lequel D sera (il est dans un état spécifique puisqu'il est déterministe). Si N a une transition qui lit x à partir d'un de ses états actuels, alors D doit avoir une transition qui lit x à partir de son état actuel. Après la lecture de x, N pourrait être dans n'importe état qui peut être atteint d'abord par une transition lisant x à partir de l'un des états actuels, puis possiblement par des transitions spontanées. Cet sous-ensemble des états de N correspond au prochain état atteint par D après la lecture de x. Etc. Si, à la fin de l'analyse, il y a parmi les états actuels possible un état qui est acceptant, alors la chaîne est acceptée.
Donc, l'automate déterministe D équivalent à un automate non déterministe N donné peut être construite de la manière suivante:
Un état x de D correspond à un sous-ensemble {s1, s2, ... sk}d'états de N.
Un algorithm systématique pour trouver un automate déterministe équivalent utilise les fonctions (mathématiques) suivantes:
La fonction є-closure(s), pour un automate non déterministe N donné, détermine le sous-ensemble des états de N qui peuvent être atteints, à partir d'un état s donné, en utilisant seulement des transitions spontanées.
Voici quelques algorithmes pour ces fonctions (voir aussi livre de Aho).
move(S, a) = {s' ׀ exists s in S and there is a transition from s to s' consuming a}
Algorithm for calculating є-closure(S):
Closure = S; Temp = S;
while (Temp != empty) {
s = get-some-element(Temp);
for each spontaneous transition from s to s' {
if (s' is not in Closure) {add s' to Closure and to Temp}
} }
Voici l'algorithm pour construire la table de transition de l'automate déterministe D équivalent à N. Note: Dstates est un ensemble d'états de D, c'est-à-dire, un ensemble d'ensembles d'états de N. À la fin de l'algorithme, Dstates contient tous les états de D; et Dtran[T, a] est le prochain état de D pour la transition à partir de l'état T avec entrée a. Voir aussi l'algorithme 3.2 du livre de Aho, Sethi et Ullman.
Pour les exemples (relativement simples) considérés dans ce cours, on peut obtenir l'automate déterministe équivalent en dessinant simplement le diagramme d'état de l'automate déterministe en l'explorant à partir de son état initial, comme indiqué par l'algorithme ci-haut. Un état non "marked" simplement indique que les transitions à partir de cet état doivent encore être explorées.
Voici un exemple. L'automate non déterministe ci-dessous (à gauche) est équivalent à l'automate déterministe (à droite). Il est aussi équivalent à l'expression régulières ((b c + a ) c )* a
Note: un automate déterministe équivalent et minimal est l'automate suivant (voir texte ci-dessous)
Un algorithme pour trouver un automate non déterministe qui accepte le langage défini par une expression régulière donnée est décrit dans le livre de Aho et al (algorithme 3.3). Le principe est très simple. Pour chaque constructeur (opérateur) d'expressions régulières on définit l'automate correspondant qui est construit à partir des automates correspondant aux sous-expressions qui font partie de l'expression donnée. Ces règles de construction sont appliqués dans un ordre qui correspond à la structure syntaxique de l'expression régulières. Par exemple, considérons l'expression e = s | t où des automate correspondant aux sous-expressions s et t sont déjà trouvés (et nommés N(s) et N(t), respectivement). Alors, il est évident que le diagramme suivant représente bien un automate (non déterministe) qui accepte le langage défini par e. (Notes: Le rond à gauche de l'oval représentant N(s) est son état initial, et le rond à droite représente son état final. Toutes les règles de construction, comme celle-ci, assurent que chaque automate construit a exactement un état acceptant.)
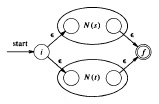
Pour plus de détails, voir algorithme 3.3, qui contient aussi l'exemple complet pour l'expression (a | b)* a b b
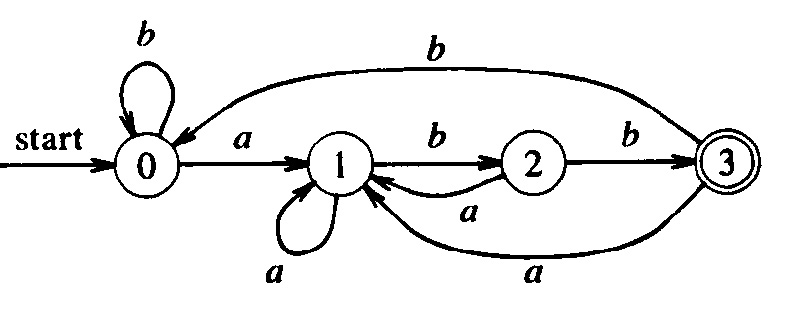
Il est peut-être surprenant que l'algorithme de construction d'automates trouve, pour l'expression (a | b)* a b b, l'automate déterministe ci-dessous qui est différent de celui montré pour l'exemple (a) ci-haut. En effet, les deux automates sont équivalents: ils acceptent le même langage. Mais ils ne sont pas identiques (dans le sense que l'on peut trouver une correspondance bi-directionnelle entre leurs états et transitions), puisque les nombres de leur états sont différents.
Definition: Un automate déterministe est minimal s'il n'existe aucun autre automate déterministe équivalent avec moins d'états.
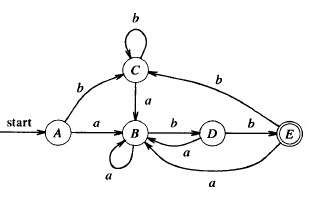
On peut alors se poser la question: Lequel des automates est plus intéressant? - Une reponse à cette question consiste à dire: celui qui est plus simple! (une approche souvent utilisé en informatique). Mais "plus simple" veut dire quoi, pour un automate? - Deux réponses possibles viennent à l'esprit: (a) celui avec le moins d'états, ou (b) celui avec le moins de transitions. On opte normalement pour la reponse (a), et cherche l'automate avec le plus petit nombre d'états. Parmi tous les automates équivalents, c'est un automate minimal. Il existe des algorithmes pour trouver un automate minimal équivalent à un automate donné (voir aussi ci-dessous). Un tel algorithme pourrait être appliqué à l’automate ci-haut pour aboutir à l’automate minimal montré plus haut pour l'exemple (a). Note: L'outil LTSA peut être utilsé pour trouver l'automate minimal pour un automate déterministe donné (voir l'exemple "accepting automata minimization.lts").
Question: Comment peut-on vérifier qu'un automate (comme celui-ci) est minimal? - Réponse: Si le langage accepté pour chaque état (pris comme état initial) est différent des autres états, alors l’automate est minimal. Inversement, si on veut trouver l'automate minimal équivalent à un automate donné, on peut procéder comme suit: déterminer les langages acceptés par chaque état; si ces langages sont identiques pour deux états alors on peut fusionner ces états en un seul, et ainsi de suite, jusqu'à ce que l'automate soit minimal. Dans l'automate ci-dessus, les états A et C sont équivalents et peuvent être fusionnés; on obtient alors l'automate déterministe de l'exemple (a).
Dernière
mise à jour: le 23 février, 2015
