Analyse syntaxique

Notes de cours pour la section 2, chapitre 3 du cours SEG
par Gregor v. Bochmann, créées en 2004, dernière revision: févr. 2015

Équations récursives de langages

Équations récursives

Vous connaissez les équations récursives de l'algèbre linéaire. Exemple:

• x1 = a11 * x1 + a12 * x2 + b1
• x2 = a21 * x1 + a22 * x2 + b2

Ce sont des équations sur le corps des nombres réels où la multiplication a un inverse, la division. C'est pourquoi on peut trouver une solution par substitution. Par exemple, de la première équation, on peut obtenir l'expression suivante pour la valeur de x1: : x1 = 1/(1-a11) * (a21 * x2 + b1). Ceci peut être substitué dans la deuxième équation qui peut ensuite être résolue pour obtenir x2.

Une opération inverse n'existe pas pour les opérateurs d'union et de concaténation qui sont utilisés pour les chaînes (e.g. expressions régulières). C'est pourquoi de telles méthodes de résolution ne peuvent pas être utilisées pour les équations de langages.

Il existe une autre méthode pour résoudre un système d'équations récursives (mais qui ne marche pas dans tous les cas). C'est par substitution itérative en commençant avec des valeurs initiales bidons pour toutes les variables. Voici un exemple: Nous considérons l'équation x = 0.5 * x + 4. On écrit x(i) pour la i-ème valeur de x obtenue dans la i-ème itération. Si on commence avec la valeur initiale x(0) = 0.0, alors on obtient la séquence suivante de valeurs pour x, où x(i) est substitué dans l'équation pour obtenir la valeur de x(i+1). Voici la séquence: x(0) = 0.0; x(1) = 4.0; x(2) = 6.0; x(3) = 7.0; x(4) = 7.5; etc. On voit que nous n'atteignons jamais la solution exacte, qui est x = 8.0, mais on s'approche à cette valeur arbitrairement près, si on continue l'itération. On dit que la valeur de x(i) converge à la solution exacte quand i tend vers l'infini (comme vous avez entendu dans des cours de mathe).

Équations récursives de langages

Nous considérons maintenant des équations entre langages formels, c'est-à-dire, les variables qui nous considérons ont des valeurs qui sont des langages - des ensembles de chaînes sur un alphabet donné - comme discuté dans la chapitre sur l'analyse lexicale. Comme discuté alors, un système d'équations de langages est normalement appelé une grammaire. Dans ce qui suit, nous utilisons la notation des ensembles comme utilisée dans le chapitre précédant pour décrire les langages formels. Notez que l'on pourrait aussi utiliser la notation BNF qui est normalement utilisée pour les grammaires.

Comme exemple, nous considérons l'alphabet A = {a, b, c}. Les langages sur A sont les sous-ensembles de A* (l'ensemble de toutes les chaînes formées par des symboles de A). Comme dans la discussion des langages réguliers, nous utilisons les opérateurs union (U) et concaténation (.) appliqués sur des langages pour obtenir de nouveaux langages. Les définitions suivantes sont de complexité variable.

Exemple 1: Voici deux exemples d'équations non récursives qui définissent des langages finis par énumération. Note: C'est comme "x = 3.2" dans les équations sur les nombres réels.

• L1 = {a, b, bb}

• L2 = {ε, aa, cba}

Exemple 2 - avec solution de point fixe : Voici un système de trois équations (sans l'utilisation de la concaténation):

• L9 = {c} U   L10
• L10 =  L9  U  {a}
• L11 =  L9  U  {a, b}

Ce système d'équations peut être résolu par substitution itérative comme suit:

• L9⁽⁰⁾ = L10⁽⁰⁾ = L11⁽⁰⁾ = Ø  (valeurs initiales)

• L9⁽¹⁾ = {c};   L10⁽¹⁾ = {a} ; L11⁽¹⁾ = {a, b}  (première itération)
• L9⁽²⁾ = {a, c};   L10⁽²⁾ = {a, c} ; L11⁽²⁾ = {a, b, c}    (deuxième itération)
• L9⁽³⁾ = {a, c};   L10⁽³⁾ = {a, c} ; L11⁽¹⁾ = {a, b, c}    (troisième itération, et toutes les iterations suivantes); nous avons atteint ce que l'on appelle un point fixe.
  

Note: Pour tout système d'équation de langages sans opérateur de concaténation, il y a toujours une solution finie obtenue par le point fixe. Pourquoi ?? - Nous allons voir cette sorte d'équations quand nous calculerons les ensembles First et Follow des grammaires LL(1) (voir plus bas).

Langages réguliers

Exemple 3: Une définition régulière est un système d'équations où chaque partie droite est une expression régulière sans récursivité. L'exemple suivant est spécialement simple parce qu'il n'utilise pas l'opérateur de Kleene:

• L1 = {a, b, bb}

• L2 = {ε, aa, cba}
• L3 = L1 . L2   U  {aa, bb}

Note: Une définition régulière peut être résolue par substitution. Dans cet exemple on obtient pour L3:

L3 = ( {a, b, bb} . {ε, aa, cba}) U  {aa, bb}

Exemple 4 - récursion à gauche: Voici une seule équation avec récursion à gauche (ce que veut dire que la variable récursive est sur le côté gauche de la concaténation):

• L4 = {a} U  L4 . {b}

Cette équation peut être résolue par substitution itérative comme suit:

• L4⁽⁰⁾ = Ø  (valeur initiale)

• L4⁽¹⁾ = {a}  (première itération)
• L4⁽²⁾ = {a, ab}  (deuxième itération)
• L4⁽³⁾ = {a, ab, abb}  (troisième itération)
• etc. - ceci continue et L4 va inclure éventuellement toutes les séquences d'un "a" suivi par n "a" consécutifs, pour toutes les valeurs de n.
• Dans ce cas, aucun point fixe est atteint après un nombre fini d'itérations, mais la valeur de L4 obtenue après chaque itération s'approche de plus en plus au point fixe qui est l'ensemble infini des chaînes défini par l'opérateur de Kleene comme suit: "{a} ({b})* ", ou par l'expression régulière " a b* " .
• Conclusion: La solution d'une seule équation avec récursion à gauche peut être définie par une expression régulière.

Une équation plus générale est la suivante: LG = L1 U LG . L2 où L1 et L2 sont des langages donnés, par exemple ceux définis ci-haut. Par substitution itérative nous obtenons:

• LG⁽⁰⁾ = Ø  (valeur initiale)

• LG⁽¹⁾ = L1  (première itération)
• LG⁽²⁾ = L1 U L1 . L2 = L1 . ({ε} U L2) - (deuxième itération)
• LG⁽³⁾ = L1 U L1 . L2 U L1 . L2 . L2 = L1 . ({ε} U L2 U L2.L2) -  (troisième itération)
• etc. - ceci continue et LG va inclure éventuellement toutes les séquences obtenues par la concaténation de n fois un élément de L2 (pour n'importe quelle valeur de n) et finalement suivi par un élément de L1. Note: La solution peut aussi être écrite avec l'opérateur de Kleene comme: LG = L1 . L2 * .

Une définition alternative de l'opérateur de Kleene

Regardons l'équation de langages ci-dessus: LG = L1 U LG . L2 , et supposant que L1 = {ε}, alors nous voyons que la solution de cette équation est L2*. On peut considérer ceci comme une définition de l'opérateur de Kleene: " L2* est la solution de l'équation LG = {ε} U LG . L2 ".

Il est intéressant de noter que l'équation LG = {ε} U  L2 . LG a la même solution. Mais ceci est une équation avec de la récursion à droite.

C'est pourquoi on peut conclure que les deux grammaires

sont équivalentes - ils définissent le même langages LG. Ceci sera utile pour l'élimination de la récursion à gauche qui est nécessaire pour la méthode d'analyse LL(1) - comme discuté plus bas.

Language non réguliers

Exemple 5: Voici un autre exemple

• L5 = {c} U  {a}. L5 . {b}

On peut développer la solution par substitution itérative comme suit:

• L5⁽⁰⁾ = Ø  (valeur initiale)

• L5⁽¹⁾ = {c}   (première itération)
• L5⁽²⁾ = {c, acb}   - (deuxième itération)
• L5⁽³⁾ = {c, acb, aacbb} -  (trosième itération) , etc.

On voit que le point fixe de cette équation consiste de toutes les chaînes qui commencent par un certain nombre de a, puis un seul c suivi par le même nombre de b (même nombre que les a's au début). On écrit souvent " aⁿ.c.bⁿ ".

Il est important de noter qu'il n'existe pas d'automate accepteur qui accepte exactement ce langage. C'est parce que pendant la séquence des a au début, l'automate doit compter le nombre des a, et chaque a supplémentaire correspond à un nouvel état de l'automate. Puisqu'il n'y a pas de limite sur le nombre de a qui peuvent arriver avant le c, le nombre d'états de l'automate ne peut pas être fini. Seulement un automate avec un nombre infini d'états pourrait faire le travail, mais ce ne serait pas un automate d'états finis. Conclusion: Ce langage n'est pas régulier (il n'y a pas d'expression régulière pour ce langage).

Encore des exemples

(1) Discuter des exemples de "grammaires à jardins"

(2) Chaque système d'équation est une grammaire. Note: L'alphabet est A = {a, b, c, d}

Les arbres syntaxiques et le sens des programmes

Un exemple: Les expressions arithmétiques

Nous considérons différentes grammaires pour une version simplifiée d'expressions arithmétiques, tel que " 3 + a * ( b -5) ".

Il paraît que la grammaire la plus simple est la grammaire-E1:

• E -> C | V | E "+" E | E "-" E | E "*" E | "(" E ")"
• C -> integer
• V -> identifier

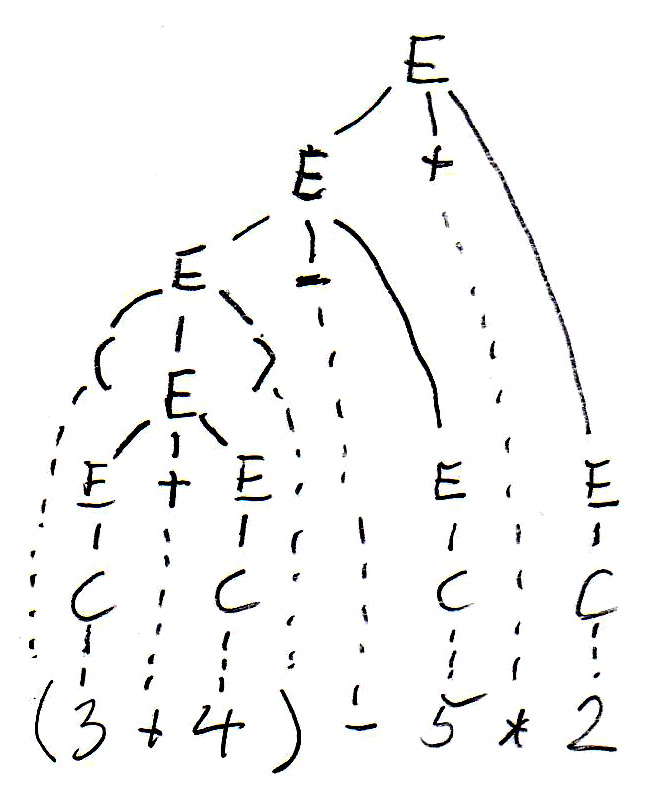
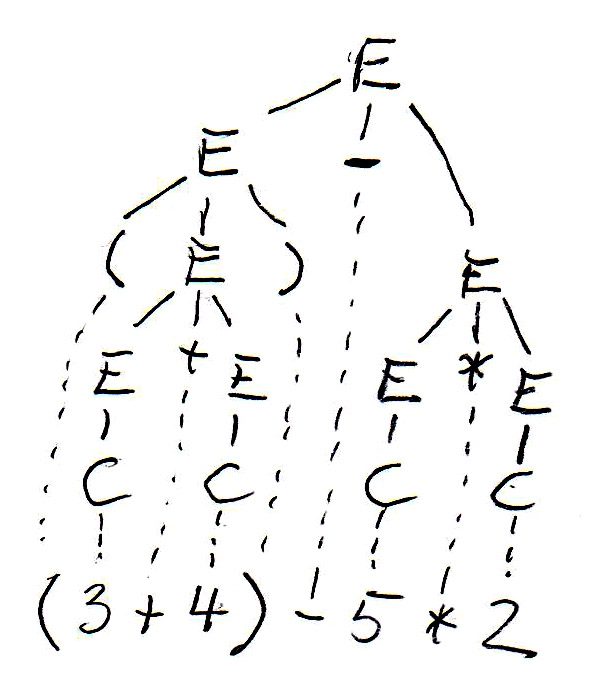
Pour l'expression " (3 + 4) - 5 * 2 ", cette grammaire permet de construire deux arbres syntaxiques différents, comme suit:

L'arbre syntaxique guide l'évaluation de l'expression (ceci est le sens de l'expression - nous voulons savoir quelle est la valeur de l'expression). Des sous-expressions entre parenthèses doivent être évaluées d'abortd - cela donne lieu à une évaluation de bas en haut sur l'arbre syntaxique.

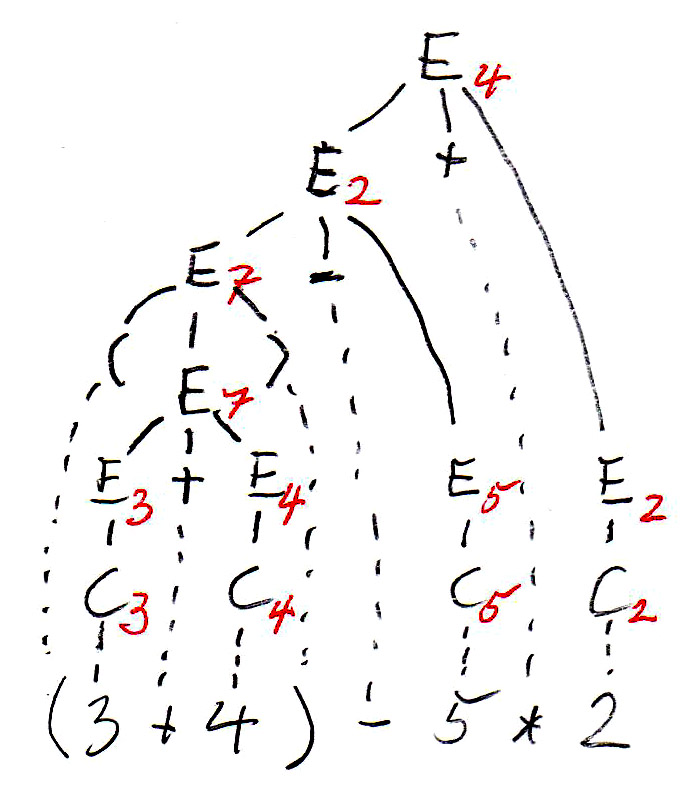
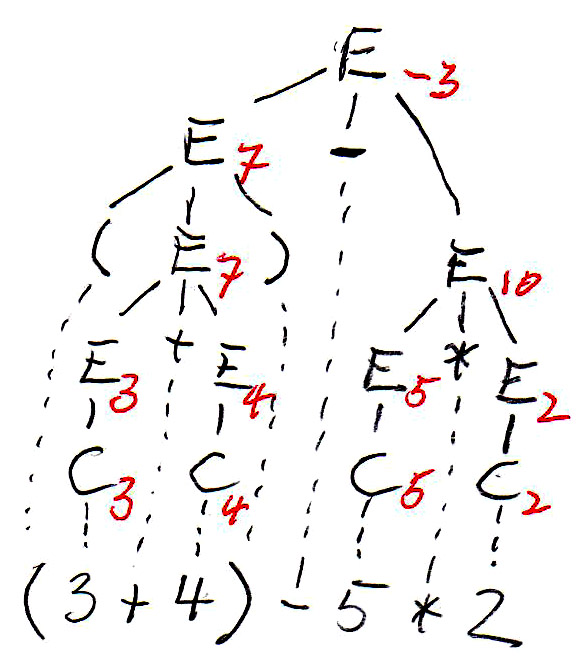
Les arbres syntaxique ont été copiés ci-dessous, et les symboles non terminaux de l'arbre (qui représentent des sous-expressions) sont annotés par leur valeurs. On voit que les deux arbres définissent des valeurs différentes pour l'expression. C'est parce que l'arbre de gauche correspond à une évaluation de gauche à droite, tandis que l'arbre de droite correspond à une évaluation de droite à gauche. On voit que cette grammaire est ambiguë puisqu'elle donne lieu à deux sens (sémantiques) pour la même expression (phrase). Pour éviter ce problème nous devons trouver une grammaire équivalente qui n'est pas ambiguë.

Ambiguité et équivalence (quelques définitions)

Équivalence: Deux grammaires sont équivalentes si elles définissent le même langage (Déjà vu plus tôt)

Phrase ambiguë: Une phrase est ambiguë si les règles syntaxiques admettent la construction de plusieurs arbres syntaxiques différents pour la phrase en question.

Grammaire ambiguë: Une grammaire est ambiguë s'il existe une phrase dans le langage défini par la grammaire qui est ambiguë.

Revenons à notre exemple d'expressions arithmétiques. La grammaire-E2 suivante n'est pas ambiguë et équivalente à grammaire-E1:

• E -> T | E "+" T | E "-" T | E "*" T
• T -> C | V | "(" E ")"
• C -> integer
• V -> identifier

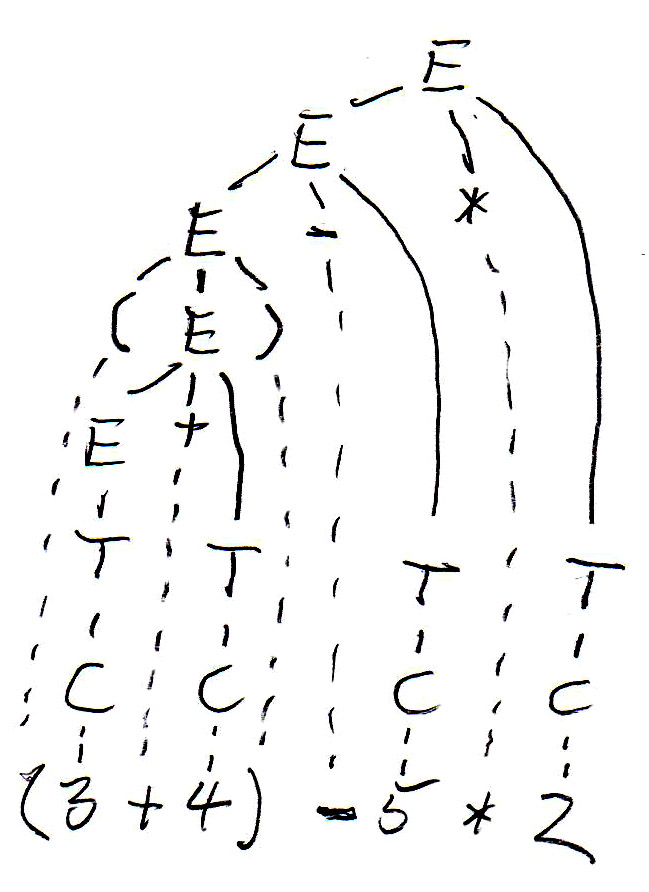
Pour l'expression " (3 + 4) - 5 * 2 ", cette grammaire donne lieu à l'arbre syntaxique suivant (voir à gauche):

Donner des priorités aux opérateurs

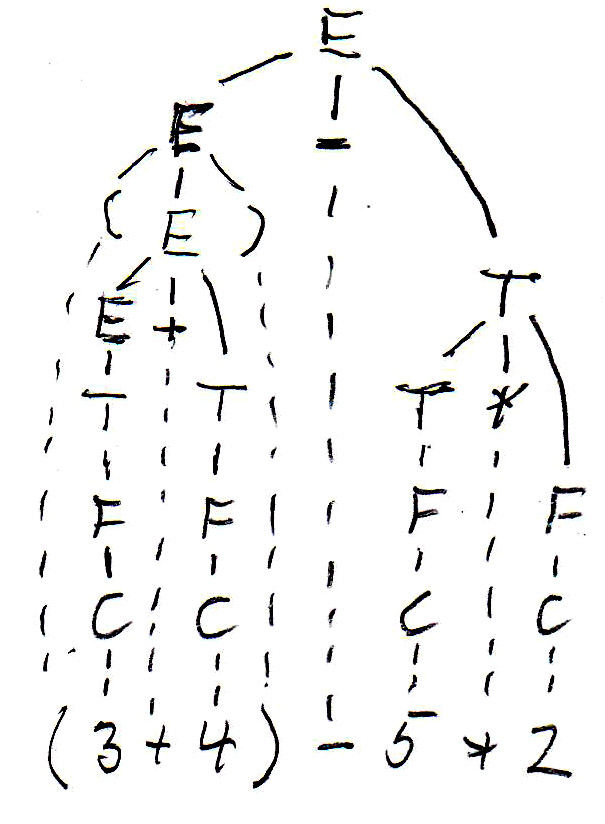Comme vous voyez en inspectant l'arbre de la grammaire-E2, cet arbre définit une évaluation de gauche à droite, mais ne donne pas de priorité de la multiplication sur + et -. Puisque nous avons toujours de l'évaluation de bas en haut, on peut introduire un autre non-terminal F, appellé "facteur", qui sera toujours en dessous du non-terminal T, appellé "term", dans une arbre syntaxique (et donc sera évalué d'abord), si on définit la grammaire-E3 suivante:

• E -> T | E "+" T | E "-" T
• T -> F | T "*" F
• F -> C | V | "(" E ")"
• C -> integer
• V -> identifier

Maintenant, on obtient pour l'expression " (3 + 4) - 5 * 2 " l'arbre syntaxique montré ci-haut (voir à droite).

Syntaxe abstraite - méta-modèles

Considérer des programmes comme des chaînes de caractères (ou chaînes d'unités lexicales) est bon pour décider si un chaîne donnée est un programme valide, mais cela ne nous dit rien sur le sens (la sémantique) du programme. Pour comprendre le sens d'un programme (ou d'une phrase parlée), il est normalement nécessaire d'analyser les différentes parties du programme (ou de la phrase) et trouver le sens des différentes composantes et leurs relations. On identifie normalement différentes classes de composantes et identifie leurs relations. Chaque classe représente normalement un concept (ou construction) du langage. Pour cette raison on utilise des fois des diagrammes de classes UML pour représenter ces aspects. Une tel diagramme de classes est souvent appelé le méta-modèle ou la syntaxe abstraite du langage.

Ces concepts sont assez intuitifs. Voici une exemple du langage Java. On considère seulement un petit sous-ensemble du langage Java: énoncés (affectation, énoncés if et while) qui utilisent des variables et expressions. Voici un diagramme de classes UML qui montre les relations entre ces concepts:

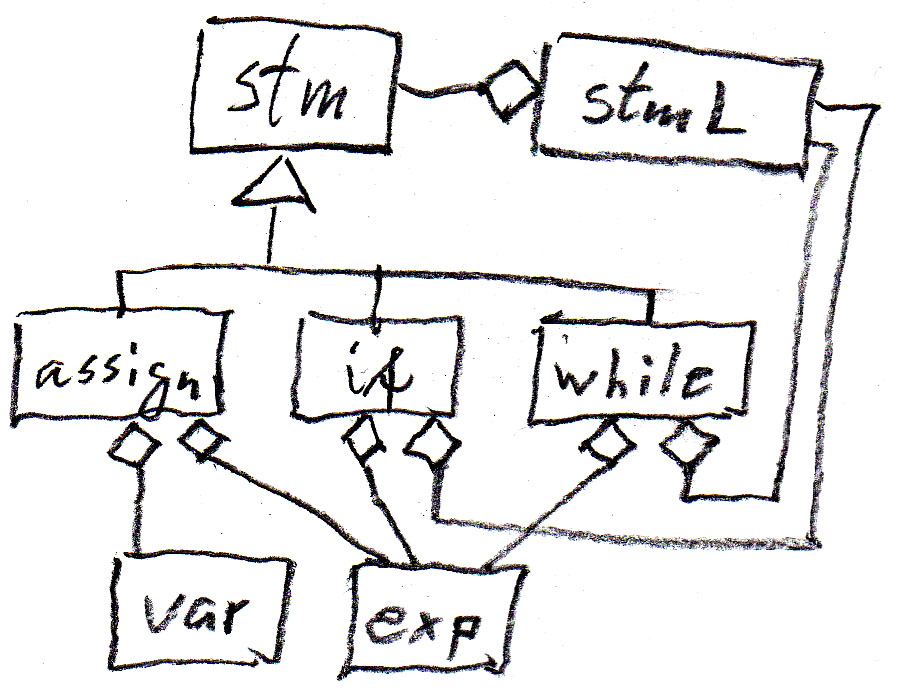
On peut représenter la relation "contient" dans le diagramme pour les règles syntaxiques qui sont montrées dans la table suivante (où assign est un énoncé d'affectation , if est un énoncé if sans else, while est un énoncé while, stm est un énoncé, et stmL est une liste d'énoncés). Il est à noter que ces règles syntaxiques sont moins abstraites que le méta-modèle puisqu'elles introduisent un ordre de gauche à droite entre les composantes.

assign --> var exp if --> exp stmL while --> exp stmL stmL --> (stm)*

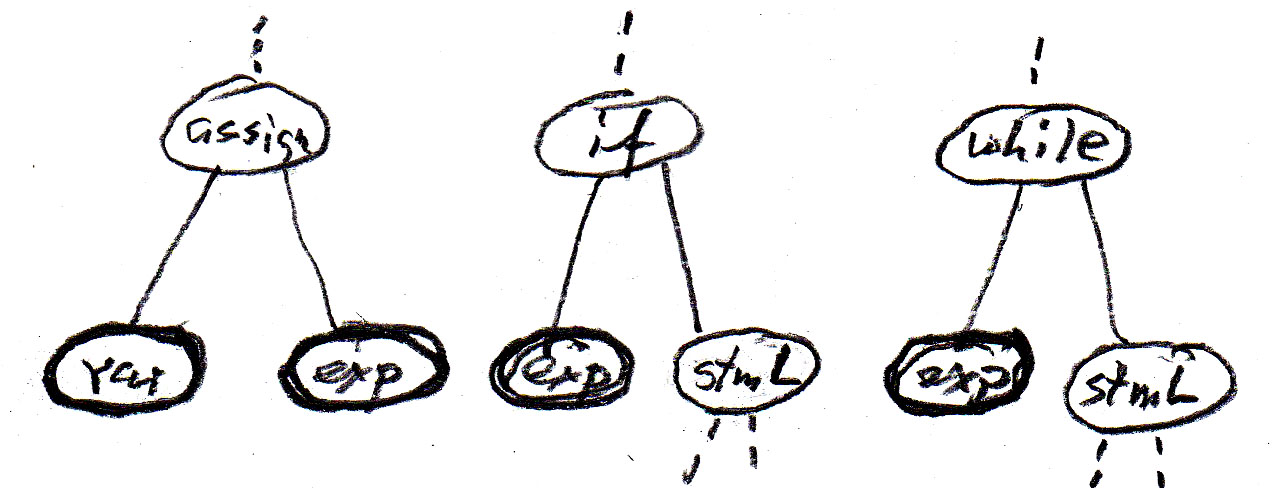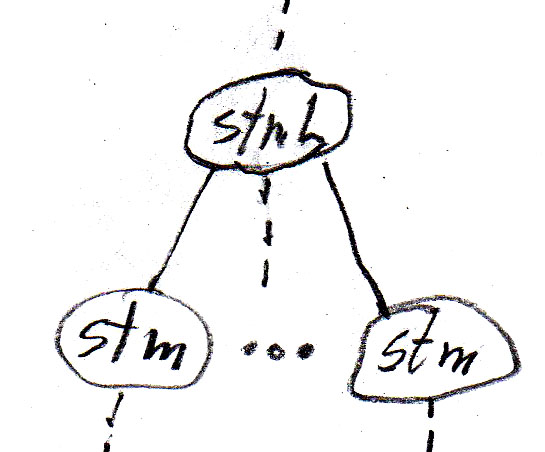Les relations d'héritage peuvent aussi être représentées par des règles syntaxiques. Le symbole --> a alors la signification "peut être de la sous-classe". Voir les règles suivantes:

• stm --> assign
• stm --> if
• stm --> while

Notez que dans ce contexte (où nous ignorons les détails des variables et expressions) les concepts var et exp peuvent être considérés comme des symboles terminaux.

Arbres syntaxiques abstraits

Nous considérons l'énoncé Java

if (b) {while (a < 10.0) {a = a + addOn();} supplement = a - 10.0;}

Utilisant la grammaire abstraite ci-haut et considérant var et exp comme terminaux, l'énoncé Java correspond à la séquence de symboles terminaux suivant: " exp exp var exp var exp " . Cette chaîne, par elle-même, n'est pas très intéressante.

Par contre, si nous utilisons les règles de la grammaire abstraite ci-haut pour construire un arbre syntaxique, le résultat est plus intéressant. Chaque règle syntaxique définit une relation possible entre des noeuds de l'arbre syntaxique, comme définie par les fragments d'arbre montrés dans la table ci-haut. Nous obtenons l'arbre suivant pour le programme exemple - il montre clairement la structure du programme - ce qui est important pour la compréhension du sens du programme.

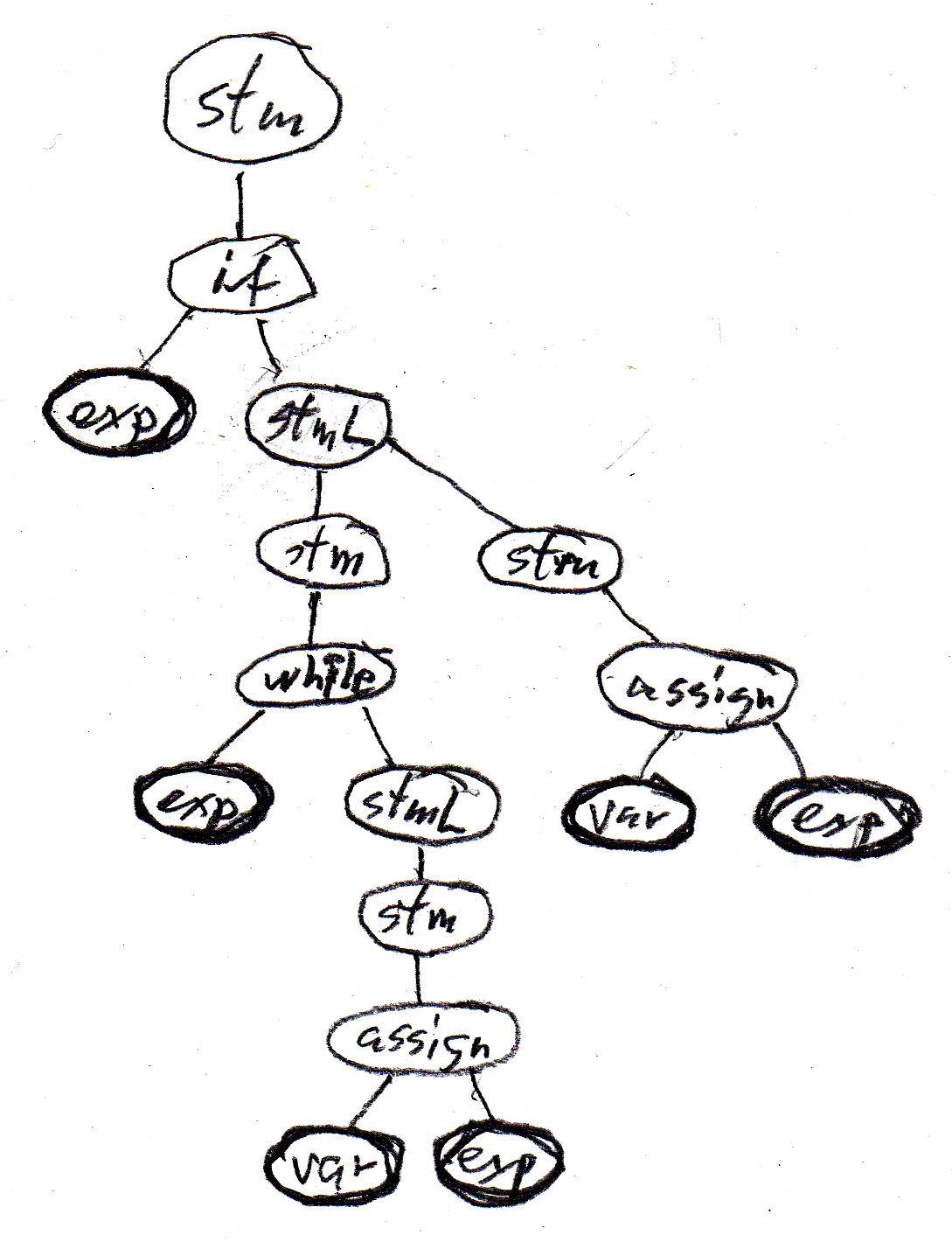
Notez que tous les arbres syntaxiques possibles peuvent être construits par substitution itérative à partir des règles syntaxiques de la grammaire.

Des règles syntaxiques plus compactes

Pour réduire le nombre de règles syntaxiques dans une grammaire, on voit souvent des grammaires où les relations d'héritage ne sont pas explicitement montrées. Par exemple, les sept règles dans notre exemple ci-dessus pourraient être remplacées par les quatre règles ci-dessous, qui forment une grammaire équivalente. Mais il est a noter que dans ce cas, les règles pour les énoncés if et while sont identiques (ce qui veut dire que la syntaxe ne peut pas les distinguer) - cette difficulté disparaît quand on ajoute le "sucre syntaxique" (voir ci-dessous).

• stm --> var exp -- assignment
• stm --> exp stmL -- if statement
• stm --> exp stmL -- while statement
• stmL --> (stm)*

Comment obtenir une syntaxe concrète (textuelle) non ambiguë ?

La grammaire abstraite est bonne pour comprendre le sens d'un programme, mais pas assez bonne pour analyser un programme donné dans la forme d'une chaîne de symboles. Par exemple, si nous changeons (dans l'exemple ci-haut) l'énoncé if en un énoncé while, la séquence des symboles terminaux est toujours " exp exp var exp var exp " - cela veut dire que nous ne pouvons pas distinguer ces deux programmes par leurs séquences des symboles var et exp. - Aussi un programme de la forme " if (b) {while (a < 10.0) {a = a + addOn(); supplement = a - 10.0;}} " aura la même séquence de symboles terminaux abstraits, quoique la structure et son arbre syntaxique abstraite sont bien différents.

Comme nous avons vu plus haut, la syntaxe abstraite pour les énoncés Java est ambiguë. Pour éviter ce problème, on définit normalement une grammaire dite syntaxe concrète qui ajoute à la syntaxe abstraite (la sémantique) certains éléments lexicaux qui doivent être inclus dans le texte du programme, et qui sont sélectionnés de manière à rendre la syntaxe non ambiguë.

Par exemple, la syntaxe concrète à gauche dans la table ci-dessous correspond à ce que les concepteurs de Java ont décidé pour la syntaxe textuelle du langage. La syntaxe concrète à droite correspond au language de programmation Pascal. Les deux langages ont la même syntaxe abstraite et méta-modèle - la même sémantique pour leurs énoncés - seulement le "sucre syntaxique" est différent. Le "sucre syntaxique" est présenté en rouge.

Avec la syntaxe concrète de Java donnée ci-dessus, l'arbre syntaxique abstraite du programme exemple devient l'arbre syntaxique du programme, comme montré ci-dessous. Cet arbre inclut la séquence des symboles terminaux qui correspondent au texte du programme en question.

Une syntaxe concrète générale: XML

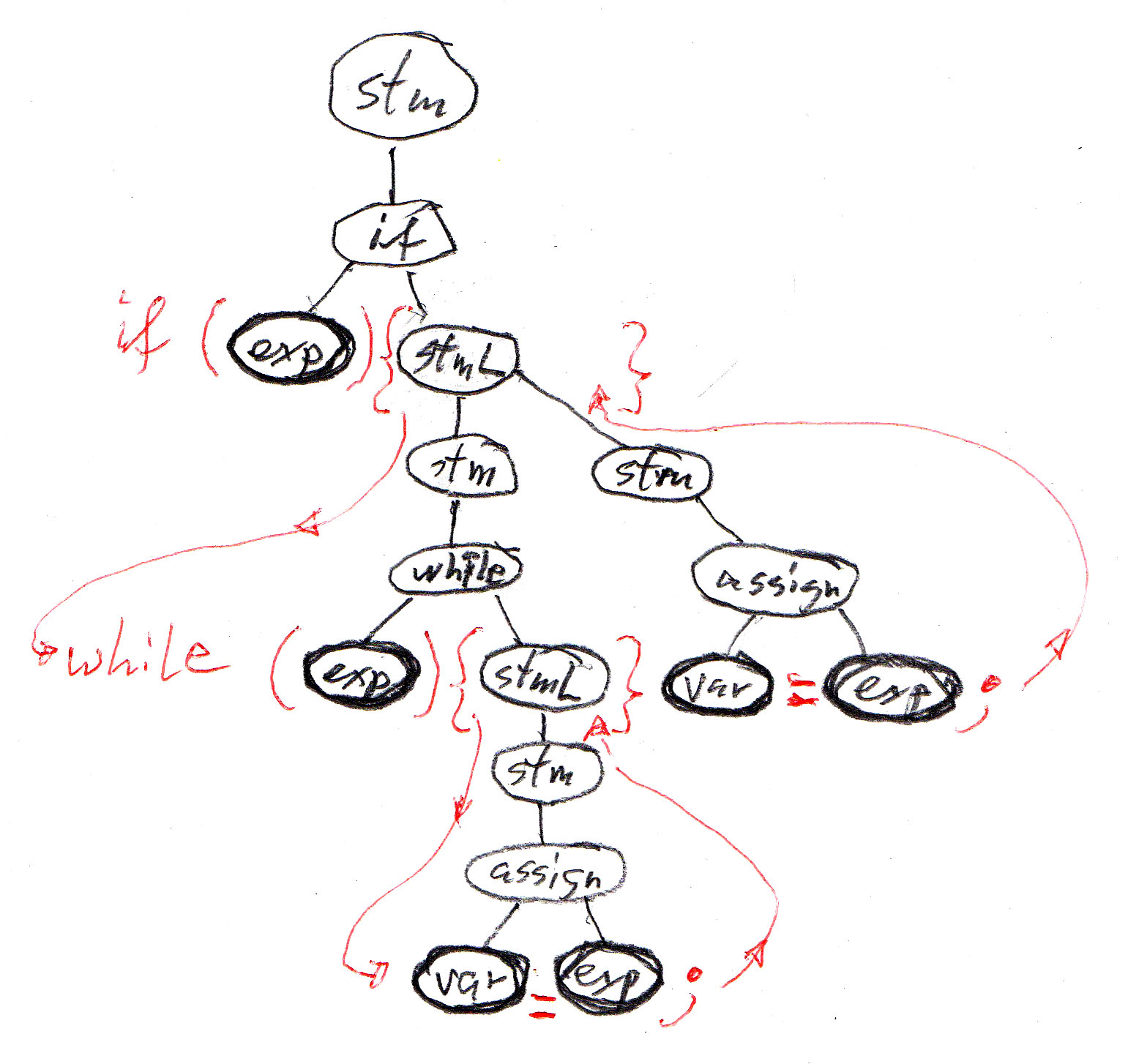
XML définit une représentation en chaîne de caractères pour des arbres abstraits. Ces arbres sont appelés DOM ("document object model"). Cette représentation linéaire est souvent utilisée pour représenter des objets ou des arbres quand ils sont transmis sur un réseau ou stocké dans une banque de données. En XML, chaque noeud de l'arbre abstrait est appelé un "element", et les éléments peuvent avoir différents types. La représentation linéaire des éléments et de leurs sous-arbres suit une convention de codage qui utilise les noms des types des éléments dans l'encodage. Chaque type d'élément peut aussi avoir des attributs, et tous les éléments ont une sorte d'attribut par défault qui est une chaîne de caractères.

L'arbre syntaxique abstrait du programme Java ci-haut, quand il est encodé en XML, pourrait être représenté comme suit (notez que l'indentation n'a pas de signification sémantique, elle est seulement introduite pour augmenter la lisibilité). Dans ce cas, les éléments n'ont pas d'attributs, ni la chaîne de caractères par défaut. Les unités lexicales <xxx> et </xxx> représentent le début et la fin d'un élément de type "xxx" et de son sous-arbre. Une unité lexicale <xxx/> représente un élément "terminal" sans sous-arbre.

• <if>
  • <exp/>
  • <stmL>
    • <while>
      • <exp/>
      • <stmL>
        • <assign>
          • <var/>
          • <exp/>
        • </assign>
      • </stmL>
    • </while>
    • <assign>
      • <var/>
      • <exp/>
    • </assign>
  • </stmL>
• </if>

ou (sans indentation): <if> <exp/> <stmL> <while> <exp/> <stmL> <assign> <var/> <exp/> </assign> </stmL> </while> <assign> <var/> <exp/> </assign> </stmL </if>

Quelques informations pour lecteur curieux (ne fait pas partie du cours)

• Comment trouver une expression régulière pour le langage accepté par un automate ?
• Introduction aux grammaire hors-contexte par exemple : définition du langage des expressions régulières

L'analyse ascendante et descendante

Voici deux grammaires pour le langage défini par l'expression régulière c c* (a | b).

Quand on analyse la phrase "c c c a" d'après la grammaire G2, on pourrait construire l'arbre syntaxique en considérant la séquence de dérivations intermédiaires (appelées "sentential forms") suivantes. À chaque étape, un non-terminal de la forme intermédiaire courant est remplacé par la partie droite de l'une des règles alternatives pour ce non-terminal. Ci-dessous, chaque ligne est une "sentential form" et le nonterminal remplacé dans la prochaine "sentential form" est montré en bleu.

• S

• c C E
• c c C E
• c c C a
• c c c C a
• c c c a

Une telle séquence est appelé "dérivation". On peut aussi considérer les dérivations d'une façon plus systématique, par exemple en considérant des dérivations les plus à gauche (où toujours le non-terminal le plus à gauche est remplacé par une partie droite de règle), ou les dérivations les plus à droite. Voici une dérivation la plus à droite pour la même phrase par rapport à la grammaire G1:

• S

• A
• C a
• D C a
• D D C a
• D D D a
• D D c a
• D c c a
• c c c a

Et voici une dérivation la plus à gauche pour la grammaire G2:

• S : il y a seulement une règle pour S; elle donne

• c C E : on applique une règle pour le premier non-terminal (de la gauche) C; choisissons la deuxième règle qui donne
• c c C E : encore une fois de même
• c c c C E : on applique une règle pour le premier non-terminal (de la gauche) C; choisissons la première règle qui donne
• c c c E : on applique une règle pour le premier non-terminal (de la gauche) E; choisissons la première règle qui donne
• c c c a

Dans le dernier cas, pour décider quelle règle à appliquer dans chaque étape, il suffisait de regarder un non-terminal à droite de la partie de la phrase déjà impliqué dans l'arbre (partiellement construit - montré en vert). On appelle cela aussi un "look-ahead" de un symbole. L'analyse a été faite en construisant l'arbre syntaxique d'en haut vers le bas; ceci est appelé analyse descendante ("top down"). Pour une grammaire quelconque, en général, on ne peut pas toujours travailler avec un "look-ahead" borné. Par exemple, si nous utilisons la grammaire G1 pour une analyse de haut en bas, il faut commencer à décider si la première ou la deuxième règle pour S sera appliquée; mais pour faire cette décision, il faut regarder jusqu'au dernier symbole de la phrase (qui peut être a ou b). Puisque les phrases peuvent être de longueur quelconque, aucun "look-ahead" de k symboles ne sera suffisant en général. L'analyse descendante avec k symboles de "look-ahead" est appelé analyse LL(k), où le premier L veut dire "from left to right" et le deuxième "left-most derivations".

Une autre méthode d'analyse populaire est LR(k) ("left to right" et "right-most derivations"). La grammaire G1 admet ce type d'analyse. L'arbre syntaxique est construit de gauche à droite d'en bas en haut (analyse ascendante). Comme exemple, on peut considérer la dérivation la plus à droite ci-haut, mais construite de bas en haut, à partir de la chaîne des terminaux. À chaque étape, seulement un prochain symbole de la chaîne d'entrée est considéré pour faire une décision sur la règle syntaxique à appliquer; voir ci-dessous, où le prochain symbole d'entrée est écrit en rouge et le non-terminal en question (dans la ligne en dessus) en bleu.

• S
• A
• C a
• D C a
• D D C a
• D D D a
• D D c a
• D c c a
• c c c a

Si une grammaire admet une analyse déterministe descendante [ou ascendante] avec k symboles de "look-ahead", on dit que la grammaire est une grammaire LL(k) [ou LR(k)].

Les méthodes d'analyse LL(k) et LR(k) sont déterministes: à chaque étape, une décision déterministe est faite à partir des règles syntaxiques et les prochains k symboles d'entrée pour construire l'arbre syntaxique. Cela implique que les grammaires sont non ambiguës, parce qu'une grammaire ambiguë permet plusieurs arbres pour une chaîne d'entrée donnée. Mais, il y a aussi des grammaires non ambiguës qui ne sont pas LL(k), ni LR(k).

Il est à noter que l'on peut toujours faire des analyses descendantes (de haut en bas) ou ascendantes (de bas en haut) si on se permet un approche non déterministe, c'est-à-dire, si on prévoit un retour en arrière dans le cas que l'on se rend compte qu'un choix précédant n'était pas le bon. Mais une telle méthode n'est pas efficace. C'est pourquoi on cherche des méthodes d'analyse déterministes. Pour admettre les méthodes LL(k) ou LR(k), la grammaire doit satisfaire certaines contraintes (voir ci-dessous).

Note: Contraire aux automates non déterministes, pour une grammaire hors-contexte qui ne permet pas l'analyse déterministe LL(k) ou LR(k), il n'y a pas d'algorithme pour trouver une grammaire équivalente qui permet une analyse déterministe. Nous avons vu dans le chapitre précédent que pour des automates non déterministes, il existe un algorithme pour trouver des automates déterministes équivalents.

L'analyse descendante LL(1) ["recursive descent parsing"]

Principe de l'analyse LL(1)

Voici un autre exemple de grammaire: Grammaire G3

• S --> A   B   C 
• A --> D   B  |  C
• B --> b  A   d  |  c
• C --> ε  |  e  C
• D --> a  |  f  A

Voici une dérivation (ci-dessous la plus gauche) de la phrase "a b e d c $" où $ représente la fin de la phrase (ou fin de fichier). Dans chaque ligne, le nonterminal le plus à gauche, qui sera remplacé par la partie droite d'une règle syntaxique dans la ligne suivante, est montré en rouge. Le remplacement est écrit en italique. À droite est un arbre syntaxique correspondant (ou les symboles terminaux sont soulignés).

Pour réaliser une analyse descendante déterministe avec un seul symbole de "look-ahead", il faut décider, à chaque ligne de la dérivation, quelle règle (alternative) doit être appliquée pour remplacer le nonterminal le plus à gauche (écrit en rouge), décision basée seulement sur le symbolle à remplacer et le prochain nonterminal qui est le symbole dans la phase donnée (ligne 10) qui est positionné en-dessous du nonterminal en question (le prochain symbole nonterminal qui ne fait pas encore partie de l'arbre syntaxique construit). Cela veut dire que le choix de l'alternative (s'il y en a plusieurs) dépend seulement du nonterminal le plus à gauche et du prochain symbole d'entrée.

Il est donc naturel de construire une table syntaxique ("parsing table") qui indique pour chaque nonterminal de la grammaire et chaque prochain symbole quelle règle syntaxique (partie droite alternative) devrait être appliquée. Notez que, pour certains nonterminaux, certains symboles d'entrée ne devraient pas arriver - si c'est le cas, il y a une erreur syntaxique. Voici la table syntaxique pour la grammaire G3 (les cellules vides correspondent à des situations d'erreur). Notez: Une entrée noire dans la table est la partie droite pour laquelle le symbole de la colonne est dans le First de la partie droite; une entrée bleue indique que le symbole de la colonne est dans le Follow du non-terminal de la ligne (et l'entrée est la partie droite qui peut engendrer la chaîne vide).

Implantation de l'analyse LL(1) - (a) approche interprétative

Une méthode simple d'implantation de l'analyse syntaxique LL(1) est la construction d'un programme interprète qui se sert des information dans la table syntaxique pour réaliser une dérivation la plus à gauche comme discutée ci-dessus. On a besoin d'un tête de lecture qui lit les symboles de la phrase donnée de gauche à droite et qui fournit à chaque instant le prochain symbole à considérer. L'autre information qui doit être gardée par l'interprète est la "sentential form" intermédiaire (i.e. le contenu de la ligne courante dans la dérivation discutée ci-dessus). Cette "sentential form" a deux parties: à gauche est le préfixe de la phrase qui est déjà analysé et à droite, il y a une séquence de nonterminaux et de terminaux qui commence par le symbole nonterminal à être remplacé. Normalement, on garde cette partie à droite dans une pile dans un ordre pour garder le nonterminal à remplacer au sommet. Cette approche est aussi utilisée dans le livre d'Aho et al. (voir ci-dessou).

Voici le programme interprète:

Voici un exemple de grammaire et la table d'analyse correspondante:

 . . . et la trace de l'exécution de l'algorithme pour la phrase "id + id * id"

Implantation de l'analyse LL(1) - (b) avec des procédures récursives (à être utilisée dans le lab-8 et devoir 3)

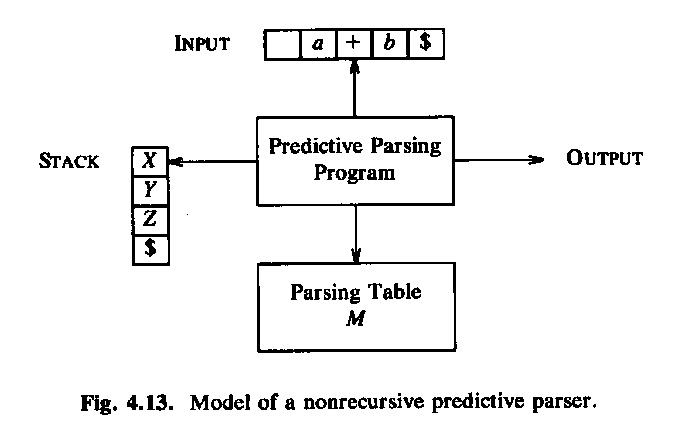
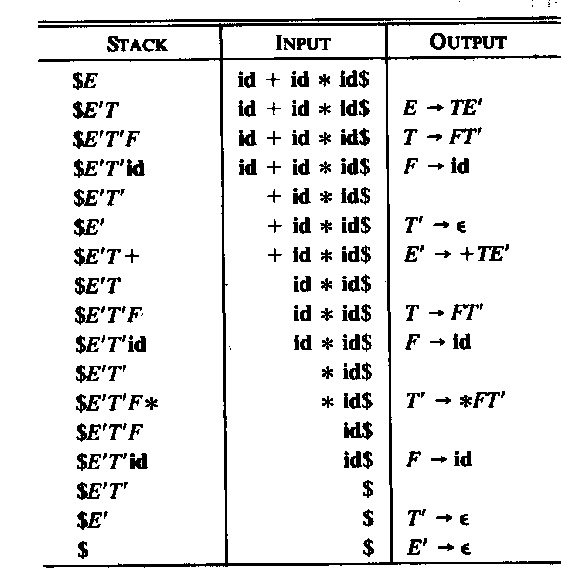
Une autre approche pour la réalisation de l'analyse syntaxique LL(1) est l'utilisation de procédures récursives, une procédure par nonterminal du langage. Les procédures appellent l'une l'autre d'une façon récursive. Chaque procédure réalise les règles syntaxiques du nonterminal en question. Par exemple, pour la grammaire G3, on pourrait écrire les procédures Java suivantes. Notez que la variable char symb contient toujours le prochain symbole terminal à considérer ("look-ahead") et la procédure next() est utilisée pour lire le prochain symbole. Le main appelle la procédure S() et vérifie, lorsque S() retourne, que le prochain symbole est la fin de la phrase ($). Notez que les chaînes comme "symb in {'a', 'b', 'c', 'e', 'f'}" ne suivent pas la syntaxe Java et devraient être recodées.

Vérification de la propriété LL(1)

Voici encore une fois la grammaire G3:

• S --> A   B   C   
• A --> D   B  |  C
• B --> b  A   d  |  c
• C --> ε  |  e  C
• D --> a  |  f  A

Notez que les modifications suivantes rendront la grammaire non LL(1):

1. La deuxième règle pour D devient D --> e A : Le choix entre les deux alternatives de A ne sera plus possible si le prochain nonterminal est (par chance) un e.
2. La deuxième règle de C devient C --> d C : Le choix entre les deux alternatives de C ne sera plus possible si le prochain nonterminal est un d. La raison est que C peut être appelé par la deuxième règle de A, et A peut être suivi par un d (voir la première alternative de B). C'est pourquoi le prochain symbole d pourrait correspondre au d de la première règle de B (alors le règle C --> ε devrait être appliquée), ou il peut correspondre au d dans le deuxième règle de C (revisée).

Pour éviter des problèmes comme sous le point (1) ci-dessus, il faut vérifier que, pour chaque nonterminal qui admet plusieurs alternatives, iil n'y a pas de nonterminal qui pourrait être le premier symbole de deux chaînes générées par deux alternatives différentes. On appele l'ensemble des terminaux qui pourraient apparaître comme premier symbole d'une chaîne générée par un nonterminal X, l'ensemble First(X). Similairement, on appele First(alternative) l'ensemble des terminaux qui pourraient apparaître comme premier symbole d'une chaîne générée par l'alternative. Pour éviter des problèmes comme sous le point (1) ci-dessus, il suffit donc d'imposer la condition suivante à la grammaire: Si un nonterminal a plusieurs alternatives, alors les ensembles First de toutes les alternatives doivent être disjoints. C'est-à-dire que les ensembles n'ont aucun élément en commun.

Pour éviter des problèmes comme sous le point (1) ci-dessus, il faut vérifier une contrainte supplémentaire pour chaque nonterminal qui peut générer la chaîne vide - parce que dans ce cas, le prochain nonterminal pourrait ne pas correspondre au First du nonterminal, mais plutôt correspondre à un symbole qui pourrait suivre la sous-chaîne générée par le nonterminal en question à l'intérieur de la phrase analysée. L'ensemble des terminaux qui pourraient suivre une sous-chaîne générée par une nonterminal X est appelée Follow(X). Pour éviter des problèmes comme sous le point (1) ci-dessus, on impose donc la contrainte suivante: Si un nonterminal X peut générer la chaîne vide, alors Follow(X) doit être disjoint de First de toutes les alternative de X. Mais cela est équivalent de dire: Si un nonterminal X peut générer la chaîne vide, alors Follow(X) doit être disjoint de First(X). Pour déterminer si un nonterminal peut générer la chaîne vide, on inclut normalement le symbole  "ε" dans l'ensemble First(X) si X peut générer la chaîne vide (même si formellement, ce symbole n'est pas un symbole terminal qui sera lu).

En conclusion, on peut dire qu'une grammaire est de type LL(1) si elle satisfait les deux conditions suivantes pour tous les nonterminaux:

• Pour tous les non-terminaux, les ensembles First de toutes les alternatives sont disjoints.

• Pour tous les non-terminaux, si le First d'une alternative contient  "ε" alors le Follow du nonterminal doit être disjoint avec le First.

Calcul des ensembles First et Follow

Note: Les règles de calcul des ensembles First et Follow sont données dans une forme qui correspond à la substitution itérative que nous avons discutée au début de ce chapitre.

Les règles de calcul doivent être appliquées d'une façon itérative jusqu'à ce qu'il n'y a plus d'ajout aux ensembles First et Follow. Initialement, on peut supposer que tous les ensembles sont vides. Les ensembles First peuvent être calculés d'abord puisqu'ils ne dépendent pas des ensembles Follow. Voici une présentation différentes de ce sujet.

First

• Pour un terminal X, l'ensemble First est: : First(X) = {X}
• Pour un nonterminal X, l'ensemble First est: : First(X) = union des ensembles First de toutes les parties droites des productions alternatives.
• Pour la partie droite d'une règle de production de la forme "ε":  First(ε) = {ε}
• Pour la partie droite d'une règle de production de la forme X₁ X₂ ... X_n:
  • First*(X1) est inclus dans First(X₁ X₂ ... X_n) où First*(Y) = First(Y) moins "ε" (si le dernier est inclus dans First(Y))
  • Si les ensembles First(X_i ) incluent "ε" pour tout i = 1 ... k, alors First*( X_k+1 ) est inclus dans First(X₁ X₂ ... X_n)
  • Si tous les ensembles First(X_i ) incluent "ε" alors First(X₁ X₂ ... X_n) inclut "ε"
  • If all sets First(X_i ) include "ε" then First(X₁ X₂ ... X_n) includes "ε"

Follow

• Pour définir plus clairement où se trouve la fin du programme, on peut introduire un marqueur, par exemple le symbole $ (supposant qu'il ne fait pas partie du programme) qui doit suivre la fin d'un programme valide. Le marqueur n'est pas vraiment un symbole du langage; pour simplifier la détection de la fin du programme, on pose Follow(S) ={$}.
• S'il y a une partie droite d'une règle de production de la forme "alpha X bêta", où alpha et bêta sont des séquences de symboles (alpha pourrait être vide, mais bêta devrait être non vide) et X est un nonterminal, alors First(bêta) est ajouté à Follow(X), excepté ε si ε est inclus dans First(bêta).
• S'il y a une règle de la forme "A -> alpha X bêta" où bêta est vide ou First(bêta) contient ε, alors Follow(A) est ajouté à Follow(X).

Exemple: Calculer les ensembles First et Follow de la grammaire G3

Calculer les ensembles Follow des nonterminaux qui génèrent la chaîne vide:

• Il faut calculer Follow(C) et Follow(A).
• Calculer Follow(A): A se trouve à la fin de la partie droite de D, c'est pourquoi Follow(A) inclut Follow(D). Dans la règle 3, A est suivi de d, c'est pourquoi d est inclus dans Follow(A). Dans la règle 1, A est suivi par B, c'est pourquoi First(B) est inclus dans Follow(A). Donc Follow(A) = Follow(D) union {d} union First(B).
  • Follow(D) = First(B) puisque D apparaît seulement une fois dans la partie droite de la règle 2 devant B.
  • C'est pourqoi Follow(A) = {d} union First(B) = {b, c, d}
• Calculer Follow(C): C apparaît à la fin de la partie droite de la règle 2 - ceci ne donne aucune contribution à Follow(C) parce que le symbole à gauche de la règle est aussi C. C est aussi à la fin de la deuxième partie droite de la règle 2 - c'est pourquoi Follow(C) inclut Follow(A). C est aussi à la fin de la règle 1 - donc Follow(C) inclut {$}. Alors, Follow(C) = {b, c, d, $}

Vérifier la propriété LL(1) et construire la table syntaxique

Une fois que les ensembles First et Follow ont été calculés, on peut vérifier si la grammaire satisfait les propriétés LL(1) discutées ci-haut. Ces propriétés assurent que dans la table syntaxique, il y a au plus une alternative dans chaque entrée de la table.

En effet, les ensembles First et Follow sont très utiles pour définir la table syntaxique. On peut suivre la procédure suivante pour remplir les entrées de la table. Pour une entrée pour le nonterminal X et le prochain symbole terminal y, le contenu de la table est déterminé comme suit:

• S'il y a une règle alternative pour X tel que y fait partie de First(alternative), alors cette entrée contient cette alternative.
• S'il y a une règle alternative pour X qui génère la chaîne vide (c'est-à-dire, "ε" est dans First(alternative) ) et y est dans le Follow(X), alors cette entrée contient cette alternative.

Transformations d'une grammaire pour la rendre LL(1)

(1) Combiner les préfixes communs: Si les parties droites de plusieurs règles de production pour le même non-terminal ont un préfixe commun (e.g. A --> a B c  |  a B A ) alors on peut incorporer les préfixes dans une seule règle nouvelle (la règle exemple devient:  A --> a B A'  et   A' --> C | A ).

(2) Éliminer la récursion à gauche: Une grammaire avec récursion à gauche (e.g. A --> A c b | a ) donne lieu à une boucle infinie lors de l'analyse par procédures récursives et pour l'interprète utilisant une table d'analyse. D'ailleurs, une telle grammaire n'est pas LL(1).

Définition: Une grammaire est récursive à gauche si elle a un non-terminal A tel qu'il est possible de dériver de A la chaîne "A Y" où Y est une chaîne de terminaux et/ou de non-terminaux quelconque.

Quand nous avions discuté la définition alternative de l'opérateur de Kleene au début de ce chapitre, nous avons vu qu'une récursion à gauche dite "immédiate" (sans non-terminal intermédiaire) peut être remplacée par une récursion à droite. La règle générale discutée avec l'exemple-4 nous donne la recette suivante pour éliminer la récursion à gauche:

•A --> Aa | b     peut être remplacé par

A -->  b A’

A’ --> a A’ |  ε

•

A --> A a1 | A a2 | … | A am | b1 | b2 |…| bn         peut être remplacé par

A --> b1 A’ | b2 A’ | …| bnA’

A’ --> a1 A’ | a2 A’ |… am A’ | ε:

Pour des cas plus complexes, on peut se servir de l'algorithme de transformation suivant (tiré du livre d'Aho et al.):

Voici des exemples

Diagrammes syntaxiques

Voici une grammaire exemple pour des expressions numériques:

1. E → T E'
2. E' → "+" T E'   |  ε
3. T → FT'
4. T' → "*" F T'   |  ε
5. F → "(" E ")"   |  id

On utilise des fois la notation BNF étendue pour définir la syntaxe, où des parenthèses, l'étoile de Kleene, et l'opérateur d'optionalité (?) sont permis. Alors une partie de droite d'une règle de production pourrait définir une expression régulière impliquant des symboles terminaux, mais aussi des non-terminaux. Par exemple, on sait que l'équation récursive " T' = "*" F T'   |  ε " a la solution T' = ( "*" F )* - notez que "*" est une symbole terminal et le * après la parenthèse fermante est l'opérateur de Kleene. C'est pourquoi les règles (3) et (4) pourraient être ré-écrites d'une façon équivalente comme

6. T = F ( "*" F )*

Diagrammes syntaxiques

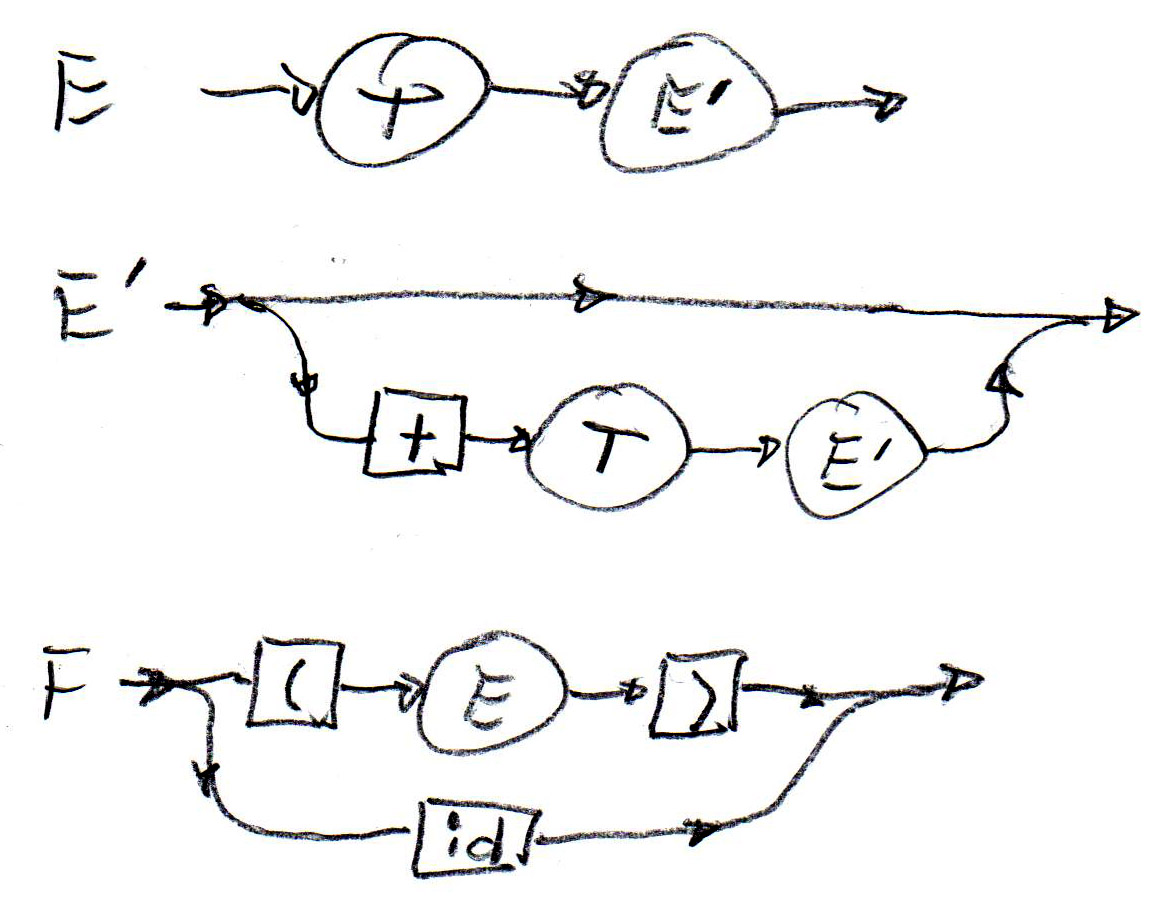
Des règles syntaxiques peuvent aussi être définies par une notation graphique similaire aux machines d'états. De telle définitions sont appelées des "diagrammes syntaxiques". Ci-dessous (à gauche) il y a de tels diagrammes pour les règles syntaxiques (1), (2) et (5) de la grammaire ci-haut. Au milieu il y a un diagramme correspondant à la règle (6). Il est important de noter que chaque diagramme est une machine d'état récursive - cela veut dire qu'il se comporte comme une machine d'états sauf que certaines transitions ne correspondent pas à la lecture d'un symbole terminal, mais représentent un appel (récursif) d'une autre machine d'états. Une machine d'états récursive correspondant au diagramme syntaxique pour T (au milieu) est montrée à droite - la flèche double représente l'appel d'une instance d'une machine-F.

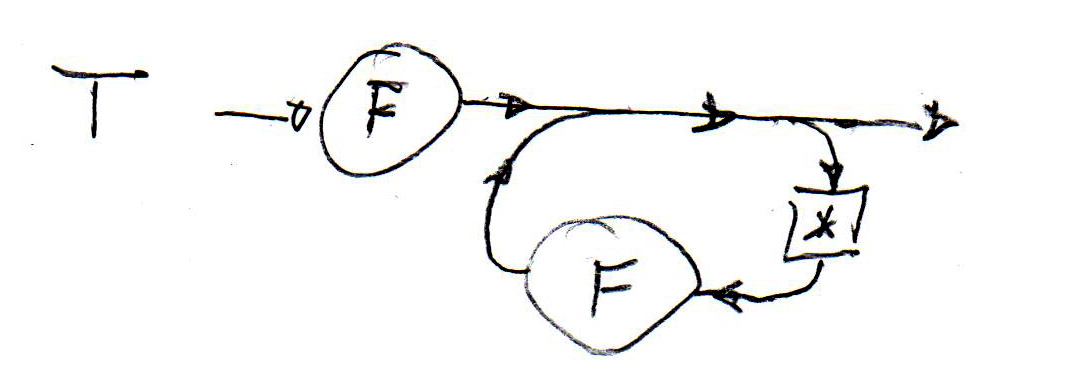Recursive automaton for T:

Notez que ces diagrammes syntaxiques (et les machines d'états récursives) peuvent être facilement implantés par des procédures récursives, comme proposé pour l'implantation de l'analyse LL(1). Par exemple, la structure syntaxique pour T montrée ci-dessus, peut être réalisée par une méthode qui contient une boucle comme suit:

• void T() { F(); while (symb == '*') { next(); F(); } }

Quand on construit un analyseur syntaxique avec des procédures récursives, on essaie souvent de réduire le nombre de procédures (à comparer avec le nombre de nonterminaux dans la syntaxe originale). En remplaçant les règles (3) et (4) par la règle (6) et en utilisant le diagramme ci-haut, on a un tel exemple de réduction.

Traitement des erreurs syntaxiques (voir ici) - ceci ne fait pas partie du cours - pour le lecteur curieux

Attributs sémantiques

Pour décrire les propriétés sémantiques des constructions syntaxiques permises par une grammaire, on se sert souvent d'attributs qui sont associés aux non-terminaux. On peut penser aux non-terminaux dans l'exemple de l'arbre syntaxique abstrait pour les expressions régulières, montré au début de cette page Web: dans cet exemple, chaque non-terminal de l'arbre est représenté par une instance d'objet en Java. Supposons que nous sommes intéressés de connaître pour chaque sous-expression l'ensemble First, c'est-à-dire l'ensemble des terminaux qui peuvent apparaître au début d'une chaîne faisant partie du langage défini par la sous-expression; par exemple, pour l'expression " a b | c a* " l'ensemble First = {a, c}. Ces ensembles First pourraient être définis comme un attribut supplémentaire de la classe Java RegExpr.

Voir section 3.5 dans le livre de Sebesta pour une explication de

• l'utilité des attributs sémantiques en général,
• les règles d'évaluation pour déterminer les valeurs des attributs sur un arbre syntaxique donné et
• l'imposition de contraintes sémantiques (dépendant des attributs sémantiques) qui expriment certains conditions sémantiques qu'un programme doit satisfaire (puisque ces conditions peuvent être vérifiées par le compilateur, on les appelle aussi des contraintes sémantiques statiques; des contraintes dynamiques sont vérifiées pendant la phase d'exécution d'un programme).

Voici des images montrant un exemple du livre: définition de la grammaire à attributs, définition + exemple d'arbre

Note: Les fonctions d'évaluation des attributs dans leur forme restreinte pour éviter des définitions circulaires, mentionnées dans [Sebesta] dans la section 3.5.3 ont été proposée la première fois dans mon article "Semantic evaluation from left to right" qui apparaissait dans le journal de prestige de l'ACM en 1976.  Voici un exemple de cet article qui montre la définition des règles de portée des déclarations dans un langage de programmation; en effet, il montre comment les informations contenues dans des tables de symboles sont passées entre les différentes parties du programme.

Exemple: les expressions - différentes grammaires et règles pour l'évaluation des attributs sémantiques

Évaluation statique veut dire évaluation pendant la phase de compilation (en opposition à évaluation pendant la phase d'exécution). L'évaluation des attributs sémantiques se fait pendant la phase de compilation. Quels attributs sont requis pour l'évaluation de la valeur d'une expression ? - Cela dépend des règles de la grammaire. Nous aimerions évaluer les attributs sémantiques pendant une passe de haut en bas à travers l'arbre syntaxique - c'est veut dire, en parallèle avec l'analyse syntaxique utilisant l'approche de descente récursive LL(1).

Nous avons vu les trois formes de règles différentes pour les expressions simples:

1. E(0) --> T | E(1) + T | E(1) - T
2. E --> T(1) ( (+ | -) T(2) )*
3. E --> T E' et E'(0) -->  ε | + T E'(1) | - T E'(1)

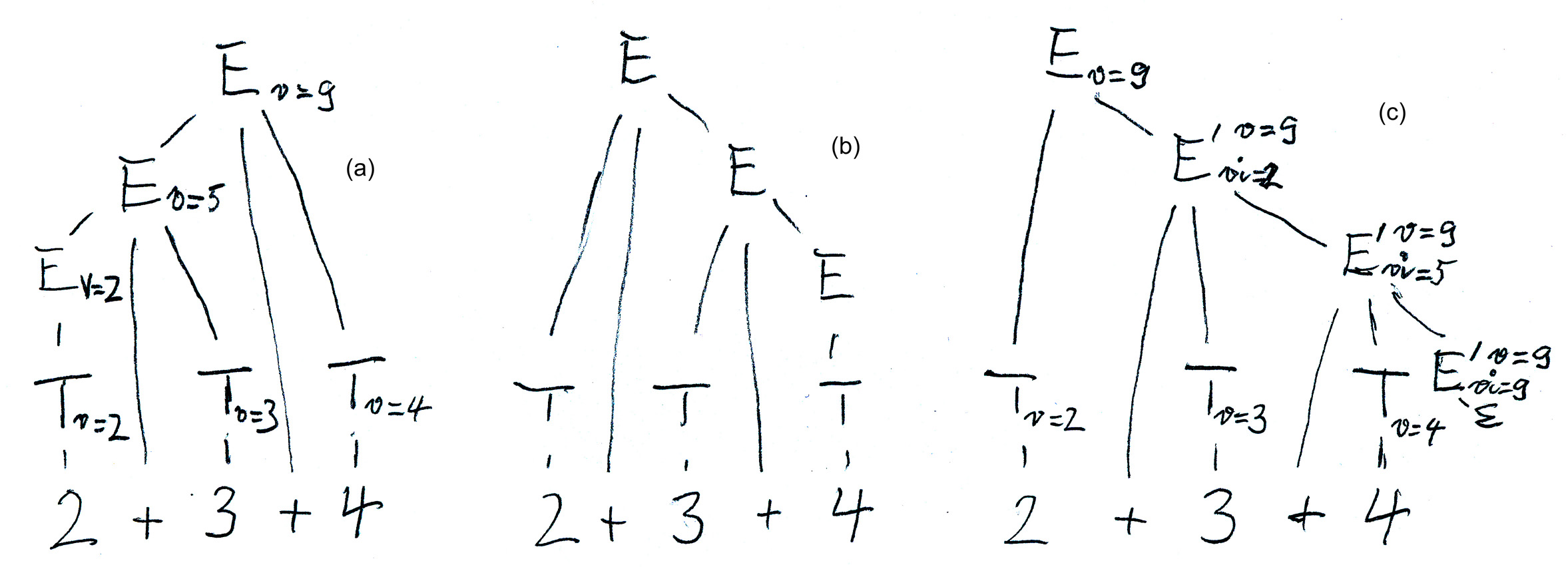
Avec la grammaire (1), nous avons un attribut synthétisé "v" (pour valeur) pour le nonterminal E qui est évalué sur l'arbre syntaxique de bas vers le haut et de gauche à droite, comme vu dans la figure (a) ci-dessous. - Mais cette grammaire n'admet pas l'analyse LL(1). - Voici les règles d'évaluation des attributs:

• pour la première alternative: v(E(0) ) := v(T)
• pour la deuxième alternative: v(E(0) ) := v(E(1) ) + v(T)
• pour la troisième alternative: simliairement.

Avec la grammaire (3), qui est obtenue de la grammaire (1) en appliquant les transformations discutées plus haut, on obtient l'arbre syntaxique montré dans la figure (b) ci-dessous. Par une évaluation des atrtributs de bas en haut, nous obtenons une évaluation de l'expression de droite à gauche, ce qui n'est pas convenable. Mais nous pouvons introduire deux attributs pour E', un attribut synthétisé appellé "v" (comme pour le nonterminal E ci-dessus), plus un attribut hérité appellé "vi" qui représente la valeur intermédiaire de l'expression évaluée jusqu'au nonterminal E' en question. Voici les règles d'évaluation (voir aussi la figure (c) ci-dessous):

• pour la règle E --> T E' : vi(E') := v(T) -- v(E) := v(E')
• pour la règle E'(0) -->  ε : v(E(0) ) := vi(E(0) )
• pour la règle E'(0) --> + T E'(1) : vi(E(1) ) := vi(E(0) ) + v(T) -- v(E(0) ) := v(E(1) )

Voici une esquisse d'une procédure qui réalise l'analyse syntaxique et en même temps l'évaluation sémantique pour E'. Notez que l'attribut synthétisé est simplement réalisé dans le programme par la valeur retournée par la procédure, et l'attribut hérité est simplement représenté par un paramètre de la procédure.

int parse_Eprime (int vi) { if(token != PLUS) {return (vi)}else {next_token(); int T_v = parse_T(); return( parse_Eprime (vi + T_v)); } }

Avec la grammaire (2): Notez que les règles d'évaluation de la grammaire (3) sont complexes. La situation devient beaucoup plus simple avec la grammaire (2). Cette grammaire a aussi l'avantage qu'elle contient un seul nonterminal, donc une seule procédure récursive (au lieu de deux, pour E et E' dans le cas de la grammaire (3)). Voici une esquisse d'une telle procédure récursive écrite en Java correspondant au diagramme syntaxique donné ci-dessous.

int parse_E () { int v = parse_T(); while (token == PLUS) {next_token(); int T_v = parse_T(); v = v + T_v; } return(v); }

Notes sur la sémantique des langages de programmation (voir ici) – ceci ne fait pas partie du cours - pour le lecteur curieux

Les quatre classes de grammaires de Chomski

Chomsky distinguait les 4 classes de grammaires suivantes (à partir de la forme la plus générale à la forme la plus restrictive):

• Grammaire générale: Les parties gauche et droite sont des chaînes de nonterminaux et terminaux (pas de restrictions). Une règle "partie gauche --> partie droite " indique que la chaîne "partie-gauche" peut être remplacée par la chaîne "partie-droite".
• Grammaire avec contexte:  Comme ci-haut, sauf que la longueur de la partie droite ne peut être plus courte que la partie gauche. Note: Souvent, la partie gauche consiste en un symbole nonterminal "dans son contexte", c'est-à-dire que le nonterminal est précédé et succédé par des chaînes de terminaux et nonterminaux qui représentent le contexte (avant et après le symbole en question). La règle ne s'applique que si le nonterminal se trouve dans le contexte donné. La partie droite contient alors les mêmes chaînes de contexte (qui ne changent pas) et une chaîne de terminaux et nonterminaux (comme dans le cas des grammaires hors-contexte) qui indiquent par quoi le nonterminal de la partie gauche sera remplacé.
• Grammaire hors-contexte: La partie gauche est un symbole nonterminal et la partie droite est quelconque. Note: Cela correspond à la notation BNF, voir toute la discussion ci-haut.
• Grammaire régulière: La partie gauche est un symbole nonterminal et la partie droite contient au plus un terminal et un nonterminal. Note: Pour chaque grammaire régulière, on peut trouver un automate d'états finis qui accepte le langage défini par la grammaire, et inversement. Donc le langage en question peut aussi être défini par une expression régulière. C'est pourquoi on appelle une grammaires de cette forme régulière.

Un langage (formel) est un sous-ensemble de l'ensemble de tous les chaînes qui peuvent être formées à partir de l'alphabet des symboles terminaux. Puisqu'en général, il n'y a pas de borne sur la longueur de ces chaînes (les phrases du langage), la plupart des langages sont des ensembles infinis. Alors la question suivante se pose: Comment peut-on caractériser un ensemble infini par une description finie ? -- On a besoin d'une représentation finie pour raisonner sur l'ensemble.

Les grammaires de Chomsky représentent une réponse possible: Chaque grammaire contient un ensemble fini de règles. Une telle grammaire est une représentation finie du langage, qui normalement est infini.

Il y a deux questions importantes en relation avec un langage donné: déterminer si une chaîne donné de symboles terminaux est un élément du langage (le problème de reconnaissance ), et l'énumération de tous les éléments du langage (le problème d'énumération). Une grammaire peut être utilisée pour répondre à ces deux questions.

Mais il est à noter que le problème de reconnaissance est non décidable pour les grammaires générales. Cela veut dire qu'il n'existe aucun algorithme (et on peut prouver qu'il ne peut y avoir un tel algorithme) qui termine et fournit la réponse à la question si une chaîne donnée fait partie d'un langage donné, défini par une grammaire de classe de Chomski générale.

Dans le cas des grammaires avec contexte, on peut énumérer les phrases d'un langage dans l'ordre de leur longueur (à partir des phrases les plus courtes vers des phrases de plus en plus longues); alors le problème de reconnaissance peut être résolu en comparant la phrase donnée avec les phrases générées par la grammaire. Si on n'a pas encore rencontré la phrase donnée lorsque la longueur des phrases générées devient plus grande que la longueur de la phrase donnée, alors la phrase donnée ne fait pas partie du langage.

Aux différents types de grammaires de Chomski correspondent différents types d'automates accepteurs, machine à états finis pour les grammaires régulières, automates avec pile pour les grammaires hors-contexte, et les machines de Turing pour les grammaires générales (pour des informations supplémentaires, voir ici).

Des problèmes non décidables

Un problème est non décicable s'il peut être montré qu'il n'existe aucun algorithme qui résoud le problème pour tous les cas possibles. - Dans un sens, on pourrait dire que le problème est "plus complexe" que les problèmes NPcomplets, parce que pour ces problèmes, il existe un algorithme, même s'il est très inefficace.

Des exemples de problèmes non décidables:

• Le problème de l'arrêt des machines de Turing (ceci est un exemple très fameux parce que dans ce contexte l'existence de problèmes non décidables a été découvert par Turing) - voici une preuve simple.
• Le problème de reconnaissance pour les grammaires générales (voir ci-dessus).
• La question si deux grammaires hors contexte sont équivalentes.
• La question si une grammaire hors contexte est abiguë.
• La question si pour une grammaire à attributs les règles d'évaluation des attributs pourraient donner lieu à une définition circulaire sur un des arbres syntaxiques possibles.

Note: Toutes les questions reliées aux langages réguliers sont décidables.

---

Revised: 2008, 2009, 2010, 2011, 2012, 2013, 16 mars 2015